Now the graph of the function \(y = f(x 2)\) can be obtained from the graph of the original function \(f\) by translating each point on the graph \(2\) units to the left You might expect a shift to the right, but if you think that the \(y\) coordinate associated with \(x = 0\) on the old graph is now associated with \(x = 2\) on the newTan(x) & Unit Circle DegreesMultiplying the values in the domain by −1 before applying the function, f (− x), reflects the graph about the yaxis When applying multiple transformations, apply reflections first Multiplying a function by a constant other than 1, a ⋅ f (x), produces a dilation If the constant is a positive number greater than 1, the graph will appear to stretch vertically
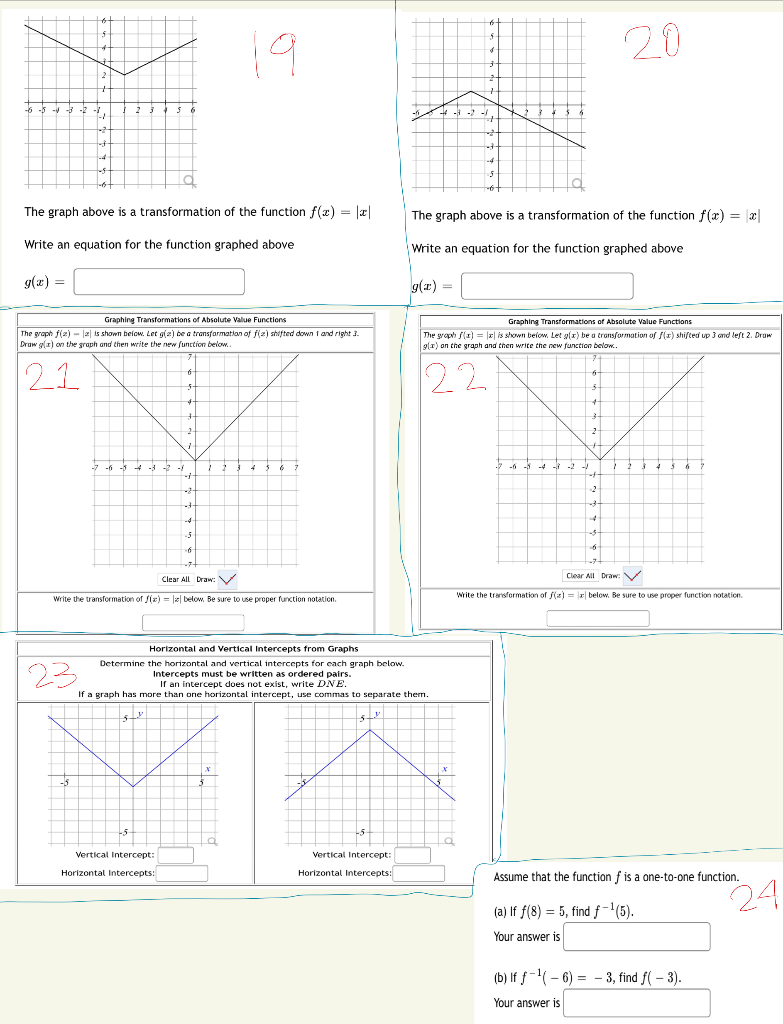
1 1 19 3 7 2 3 5 1 4 7 The Graph Above Is A Chegg Com
How to graph f'
How to graph f'- · The Corbettmaths Practice Questions on Transformations of Graphs Videos, worksheets, 5aday and much moreDescribe the Transformation f (x)=e^x f (x) = ex f ( x) = e x The parent function is the simplest form of the type of function given g(x) = (e)x g ( x) = ( e) x The transformation from the first equation to the second one can be found by finding a a, h h, and k k for each equation y = abx−h k y = a b x h k




01 Transformations Of Graphs
We're talking about graphing transformations Let's start with an easy transformation y equals a times f of x plus k Here's an example y equals negative one half times the absolute value of x plus 3 Now first, you and I ide identify what parent graph is being transformed and here it's the function f of x equals the absolute value of x · so this red curve is the graph of f of X and this blue curve is the graph of G of X and I want to try to express G of X in terms of f of X and so let's see how they're related so we pick any X and we could start right here at the vertex of f of X and we see that at least at that point G of X is exactly one higher than that so G of two I could write this down G of two G of two is equal to isDescribe the Transformation f(x)=x^21 The parent function is the simplest form of the type of function given The horizontal shift depends on the value of The horizontal shift is described as The graph is shifted to the left units The graph is shifted to the right units In this case, which means that the graph is not shifted to
Transformations of Functions Describe the affects of the following graph transformations 𝑦=𝑓(𝑥10) Left 10 units 𝑦=3𝑓(𝑥) Stretch by factor of 3 on yaxis 𝑦=𝑓(2𝑥) Squash by factor of 2 on x · What do you notice about the relationship between the graphs of y = f(x) and y = f(x 2)????Graphing Transformations of Logarithmic Functions As we mentioned in the beginning of the section, transformations of logarithmic graphs behave similarly to those of other parent functions We can shift, stretch, compress, and reflect the parent function y = l o g b ( x) \displaystyle y= {\mathrm {log}}_ {b}\left (x\right) y = log
8 rows · A horizontal shift means that every point (x,y) on the graph of f (x) is transformed to (xWhen looking at the equation of the transformed function, however, we have to be careful When functions are transformed on the outside of the \(f(x)\) part, you move the function up and down and do the "regular" math, as we'll see in the examples belowThese are vertical transformations or translations, and affect the \(y\) part of the functionThe graph of \(y=f(x)\) is a reflection of the graph of \(y=f(x)\) across the \(x\)axis The graphs of \(f(x)=x5\) and \(g(x)=x5\) are shown in Figure 569 Notice that the two lines are reflections across the \(y\)axis The graphs of \(f(x)=x5\) and \(g(x)=(x5)\) are shown in Figure 5610
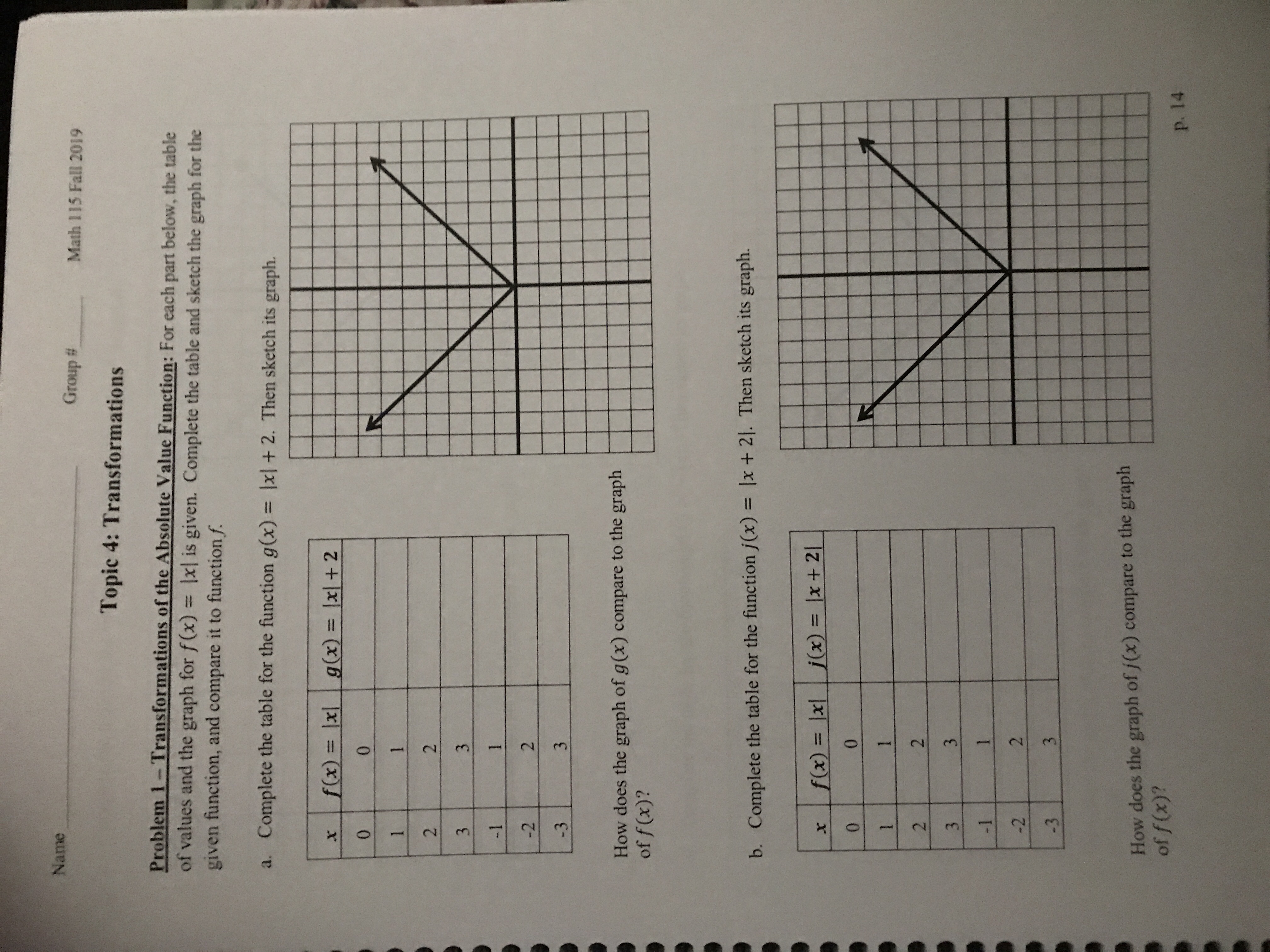



Answered Name Group Math 115 Fall 19 Topic Bartleby
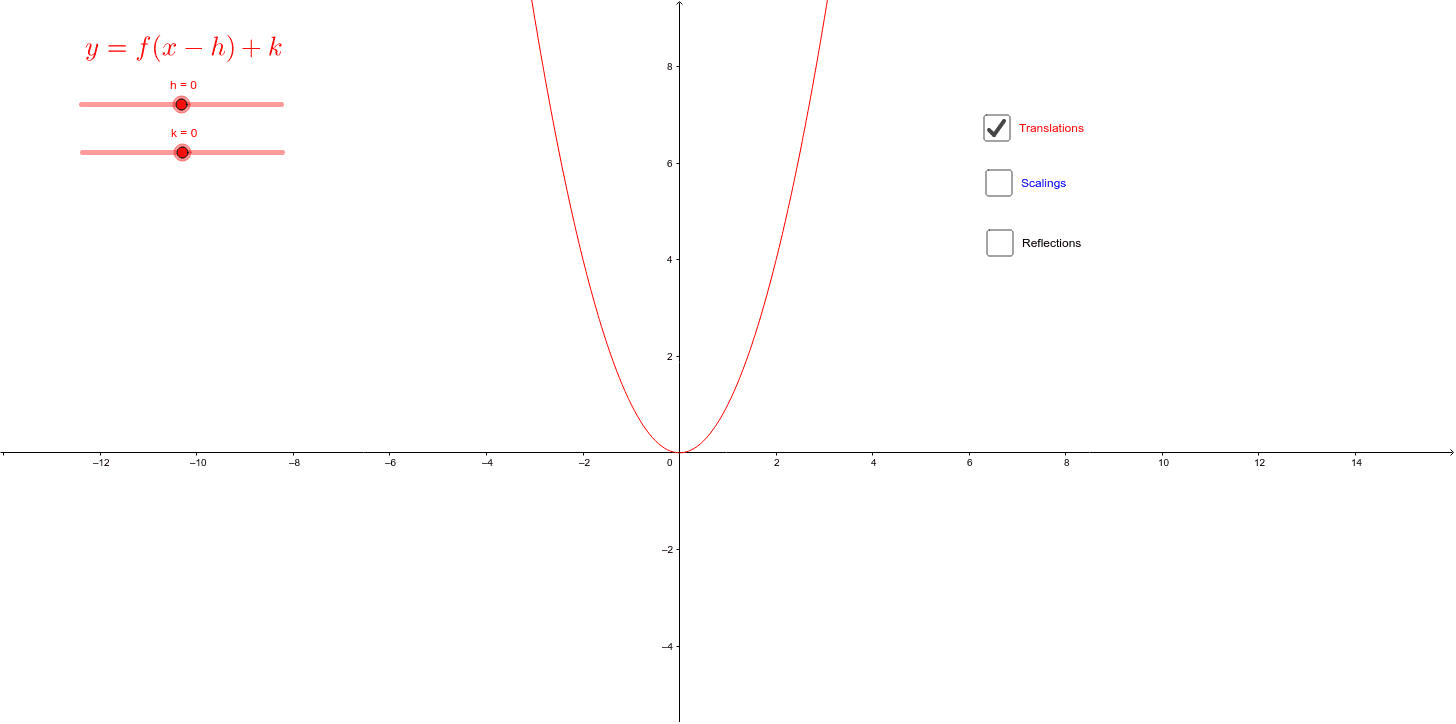



Transformations Of Functions And Graphs Geogebra
This type of graphing transformation can be written as y = f (x h) For this graphing transformation, we shift the graph horizontally by h units We should also know how to recognize vertical shifts and scaling, reflections, and horizontal compression functions transformations horizontal shift end pointGraph transformations Given the graph of a common function, (such as a simple polynomial, quadratic or trig function) you should be able to draw the graph of its related function The graphI only know that the roots of f ( x) will become VA value of 1 / f ( x) and VA values of f ( x) becomes the zeros of 1 f ( x) and that if f ( x) > 0 , then 1 f ( x) > 0 such that f ( x) → 0 1 f ( x) → ∞ and f ( x) → ∞ 1 f ( x) → 0 graphingfunctions transformation Share edited May 29 '13 at 339 Ben



Trasformations By Graph Paper Teacher Guide




01 Transformations Of Graphs Cartesian Coordinate System Mathematical Relations
The standard form of a quadratic function presents the function in the form latexf\left(x\right)=a{\left(xh\right)}^{2}k/latex where latex\left(h,\text{ }k\right)/latex is the vertex Because the vertex appears in the standard form of the quadratic function, this form is also known as the vertex form of a quadratic function The standard form is useful for determining how the graphGraph Transformations A transformation is something that is done to a graph/function that causes it to change in some way This topic is about the effects that changing a function has on its graph There are two types of transformation translations and reflections, giving 4Graph transformation is the process by which an existing graph, or graphed equation, is modified to produce a variation of the proceeding graph It's a common type of problem in algebra, specifically the modification of algebraic equations Sometimes graphs
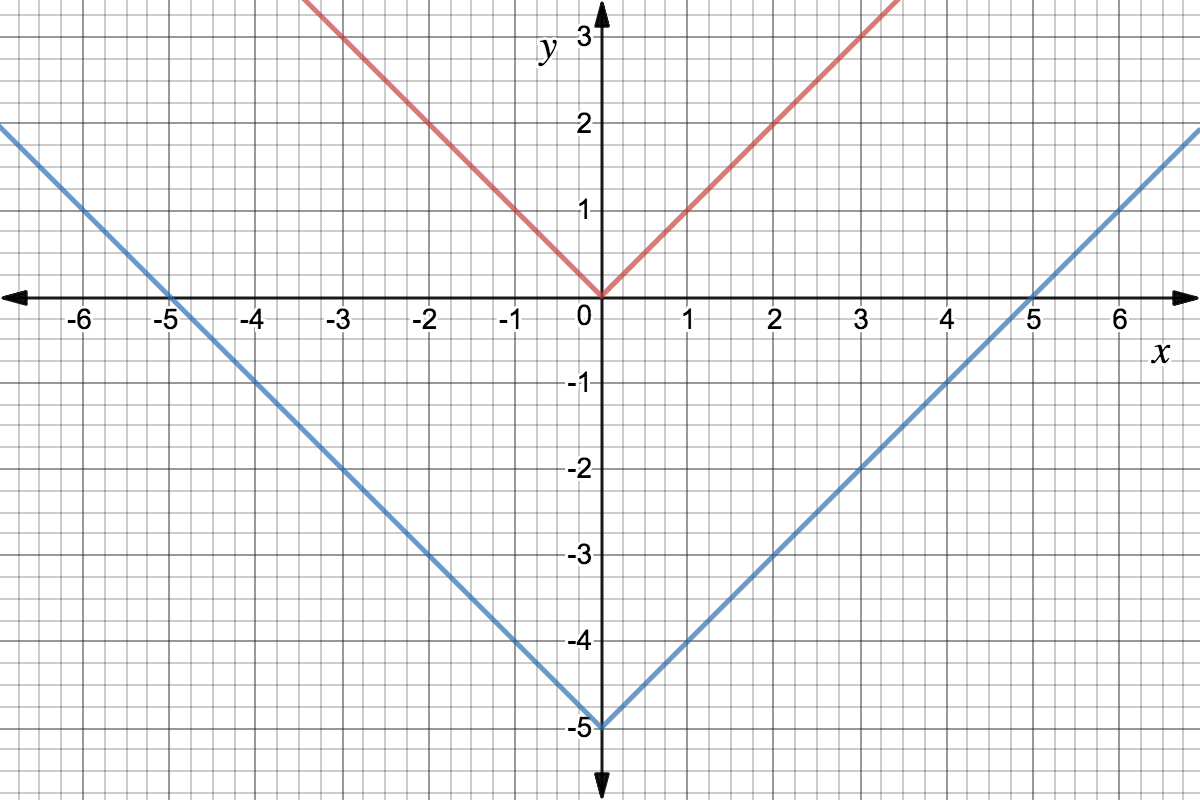



What Is A Function Transformation Expii




Horizontal And Vertical Graph Stretches And Compressions Video Lessons Examples And Solutions
Transcribed image text (5 points each) The graph of y = f(x) is given below Perform the transformations to obtain y = f(23) 4 (a) In words, state the transformations done to y = f(x) List the transformations in the order they occur · Color White Black Red Green Blue Yellow Magenta Cyan Transparency Opaque SemiTransparent Background Color Black White Red Green Blue Yellow Magenta Cyan Transparency Opaque SemiTransparent Transparent Window Color Black White Red Green Blue Yellow Magenta Cyan Transparency Transparent SemiTransparent Opaque Font Size · Last Updated June 7, 19 Graphing a function is not as simple as creating a table and plotting those points Functions can get very complex and go through transformations, such as flips, shifts, stretching and shrinking, making the usual graphing techniques difficult
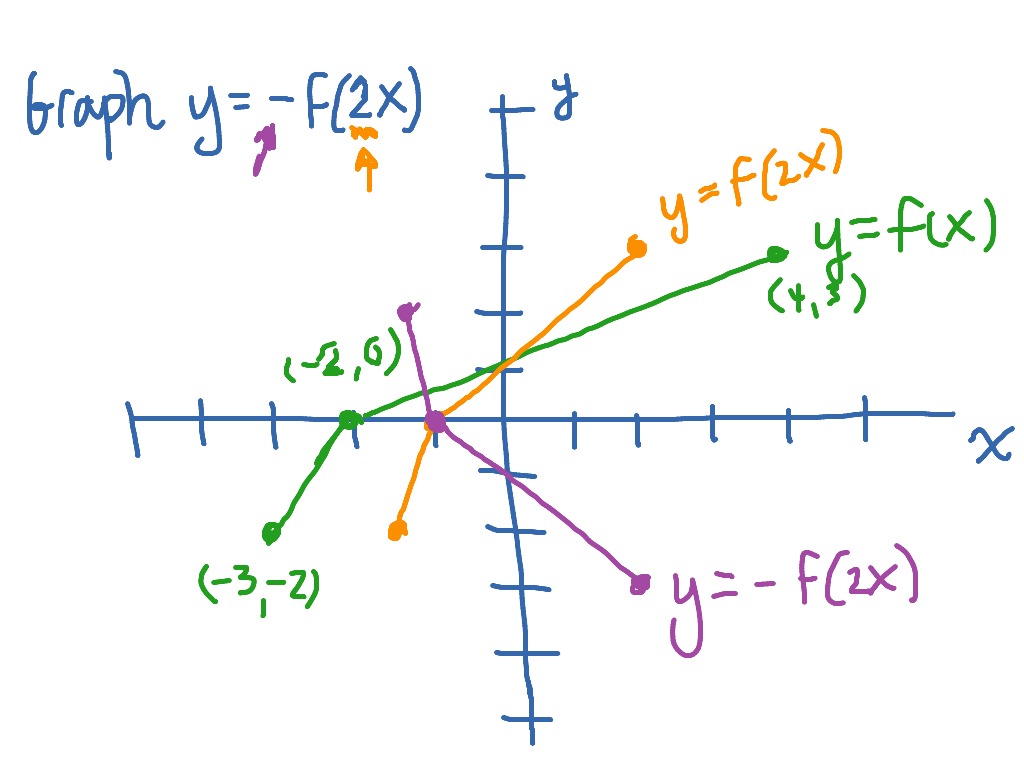



Graphing Y F 2x As A Transformation Of Y F X Math Showme




Transforming The Graph Of A Function By Shrinking Or Stretching Youtube
The graph of y = f (x) is the graph of y = f (x) reflected about the yaxis Here is a picture of the graph of g(x) =(05x)31 It is obtained from the graph of f(x) = 05x31 by reflecting it in the yaxis Summary of Transformations To graph Draw the graph of f and Changes in the equation of y = f(x) Vertical Shifts y = f (x) c · Graph Transformations Author hnees Topic Function Graph Absolute Value Transformations Exponential Parent Function Transformation of Logarithms Exploring Quadratic Functions Functions transformationssquare root, quadratic, abs value Position vs time graphs controlling velocity;Graph Transformations of y = f (x) (Easy Trick!) GCSE Edexcel Maths 91 Graph Transformations of y = f (x) (Easy Trick!) GCSE Edexcel Maths 91 If playback doesn't begin
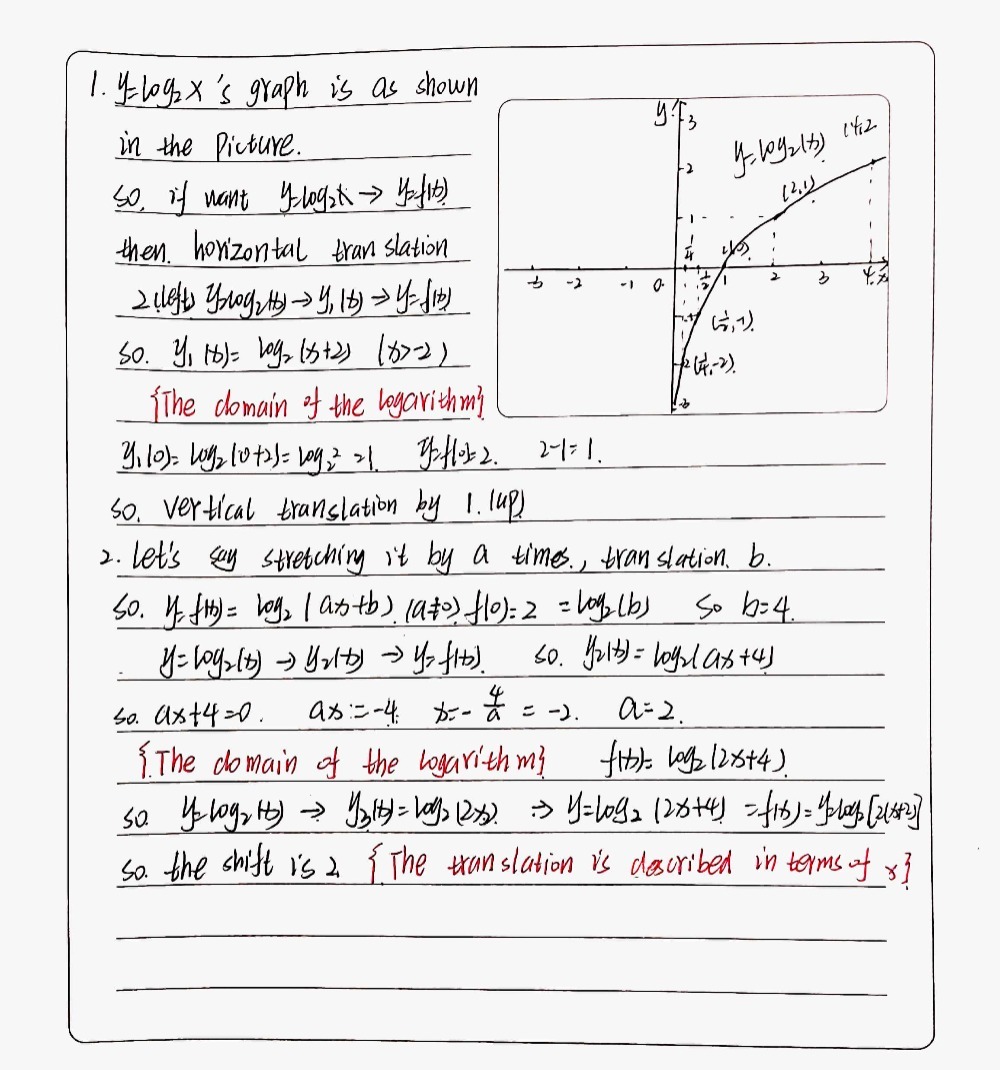



Part 1 The Graph Of Fx Is Shown It Goes Through Gauthmath
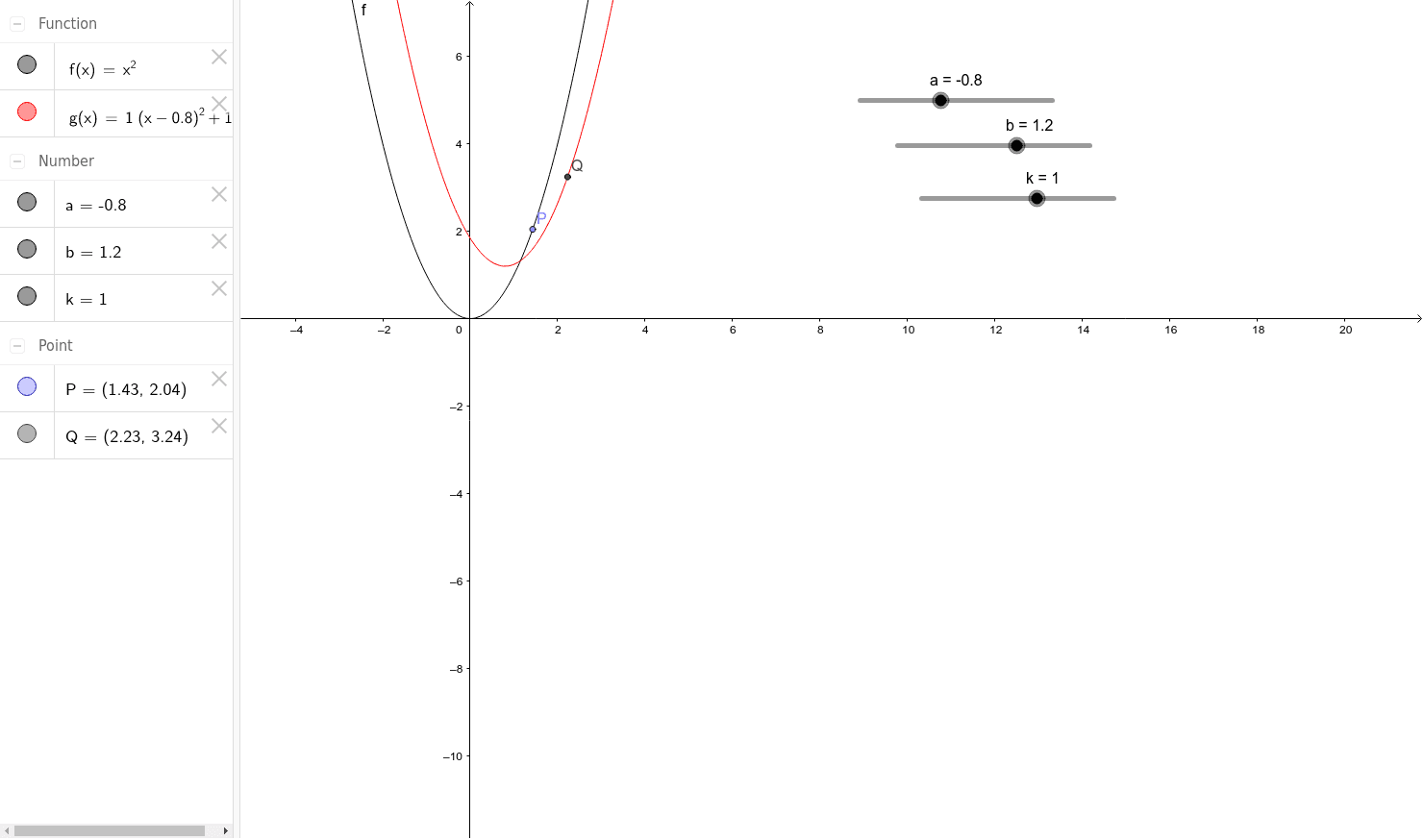



Graph Transformation Geogebra
That is, the graph moves away from xaxis or towards xaxisF f in two ways f ( x 1) f ( x 1) is a change on the inside of the function, giving a horizontal shift left by 1, and the subtraction by 3 in f ( x 1) − 3 f ( x 1) − 3 is a change to the outside of the function, giving a vertical shift down by 3 The transformation of the graph · y=f(x) will indicate that the graph has reflected about the origin If I have f(x)=(x) 3 , then the graph would be reflected about the yaxis Try to experiment on these transformations by using a graphing utility such as Desmos , Symbolab , GeoGebra




Transformations Of Graphs Edexcel Igcse Maths Revision Notes
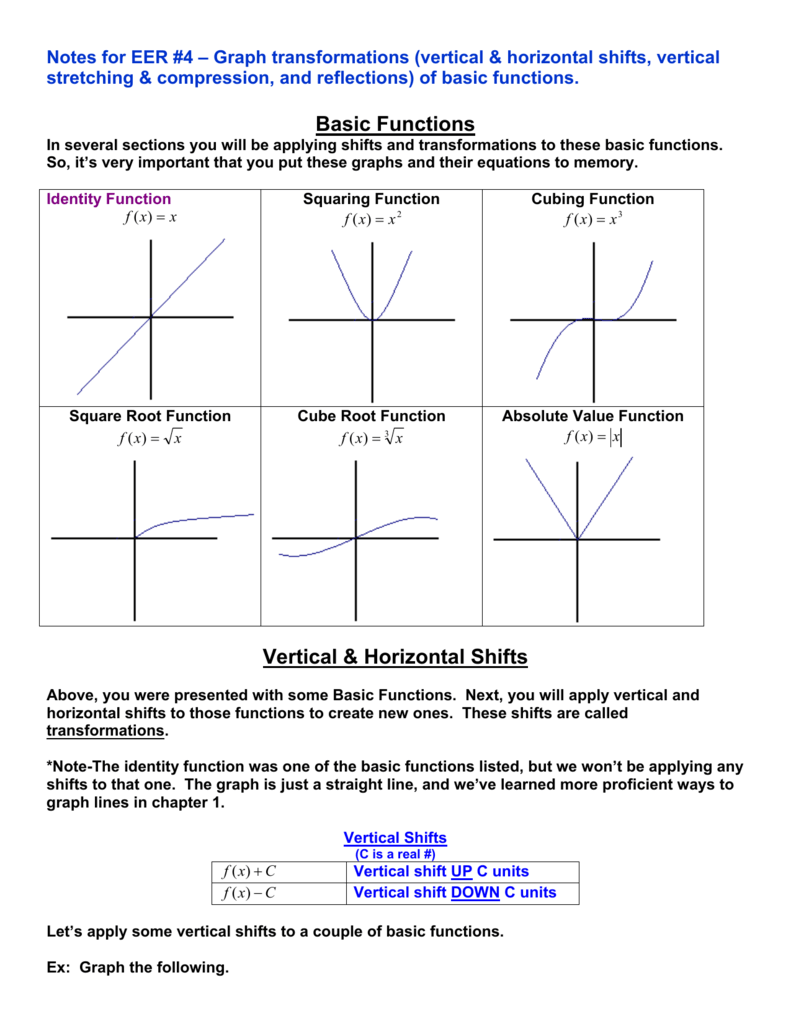



Basic Functions Vertical Horizontal Shifts
A function transformation takes whatever is the basic function f (x) and then "transforms" it (or "translates" it), which is a fancy way of saying that you change the formula a bit and thereby move the graph around For instance, the graph for y = x2 3 looks like this This is three units higher than the basic quadratic, f (x) = x2These transformations are called horizontal stretches, crunches or dilations They horizontally stretch ( a < 1) or squeeze ( a > 1) the graph of the given function The parameter a can be added to or subtracted from the output y after the rule f is applied y = f (x) becomes y = f (x) ± a These transformations are called vertical shifts orGraph Transformations Loading Graph Transformations Graph Transformations Log InorSign Up f x = 2 x 3 − 6 x 2 2 1 y = f x 2 Starting at y=2f(x), click on the circle to reveal a new graph Describe the transformation Click again to remove and try the next function 3 y = 2 f x 4 y = f x 2 5 y = f x −
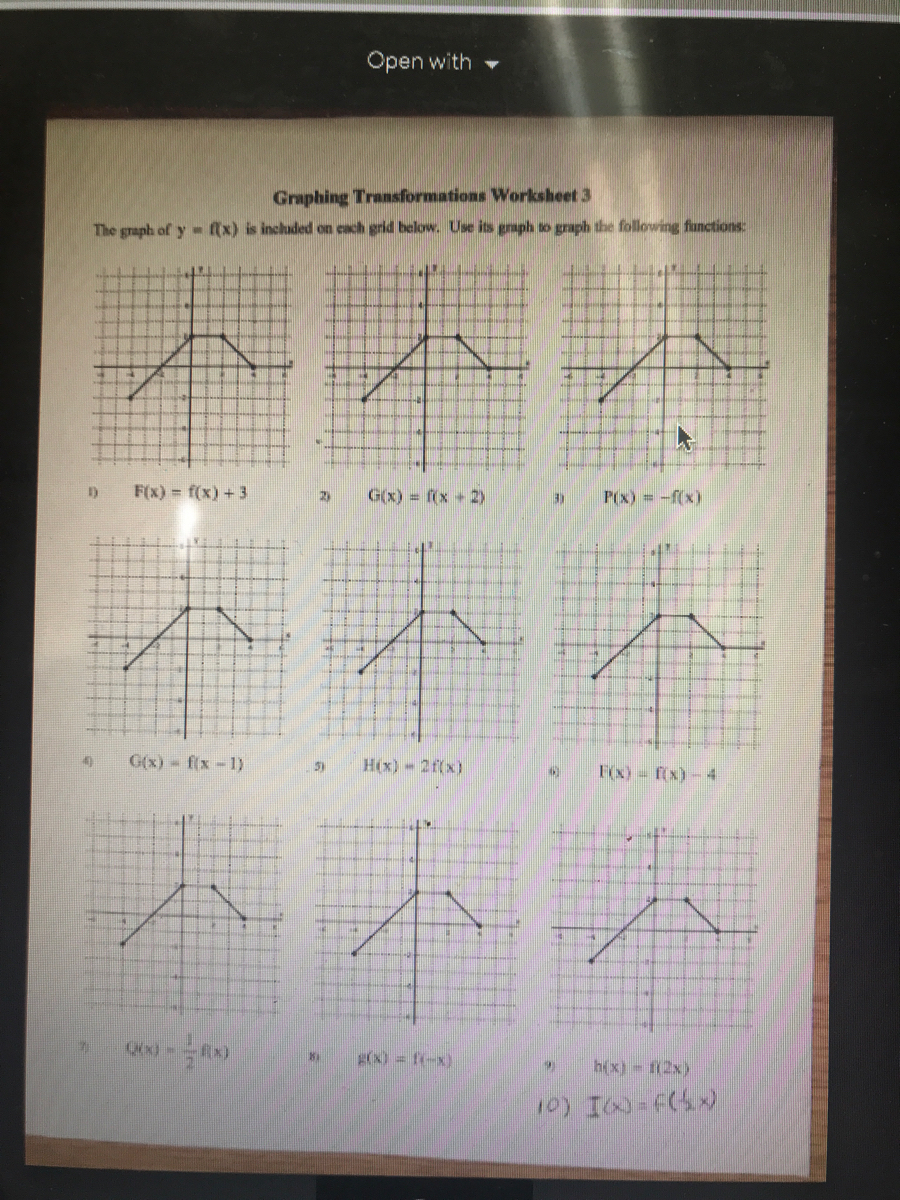



Answered Graphing Transformations Worksheet 3 Bartleby




Transformations Of Functions Mathematics Learning And Technology
· The values of f(x) are the y values on the graph of y = f(x) For example, using the points indicated on the graph of f, we can make the following table In general, if (a, b) is on the graph of y = f(x), then f(a) = b, so g(a) = f(a) 2 = b 2 Hence, (a, b 2) is on the graph of g · 000 / 0 Live • Video tutorial on Graph Transformations y=3f (x) and y=f (2x) Tes classic free licence Report this resource to let us know if it violates our terms and conditions Our customer service team will review your report and will be in touch £000Each of these functions above can have transformations applied to them A transformation is an alteration to a parent function's graph There are three types of transformations translations, reflections, and dilations When a function has a transformation applied it can be either vertical (affects the yvalues) or horizontal (affects the xvalues) Below is an equation of a function that




Transformations Of Graphs Edexcel Igcse Maths Revision Notes




2 4 Transformations Of Functions And Graphs Ppt Download
Functions of graphs can be transformed to show shifts and reflections Graphic designers and 3D modellers use transformations of graphs to design objects and images Part of Maths AlgebraTransformation of f (x)=sin (x) Change sliders a, b, c, and d to see the effects of the transformations on the parent function · IBDP Past Year Exam Questions – Transformation Q1 N10P2 The diagram shows the graph of a linear function and a quadratic function On the same axes sketch the graph of f g Indicate clearly where the x intercept and the asymptotes occur 5 marks Q2 M08P2TZ2 The graph of y = f x for – 2 ≤ x ≤ 8 is shown
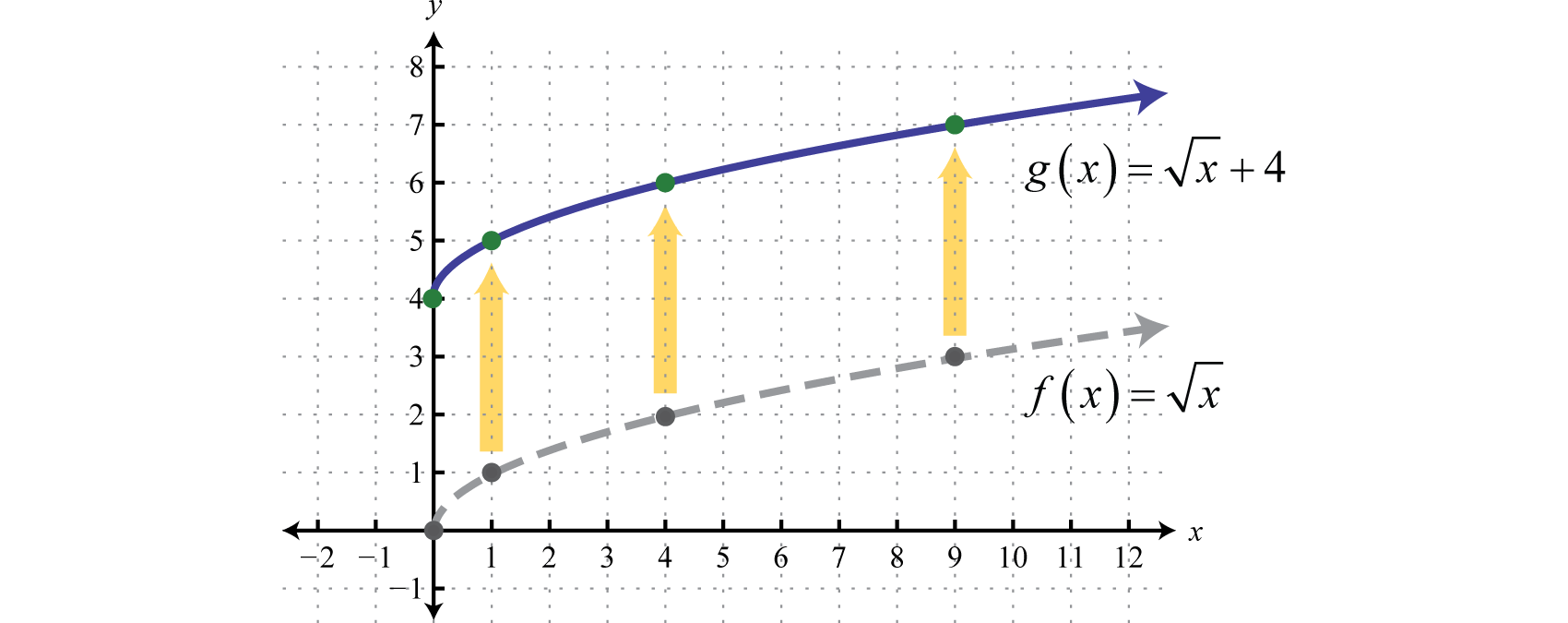



Using Transformations To Graph Functions
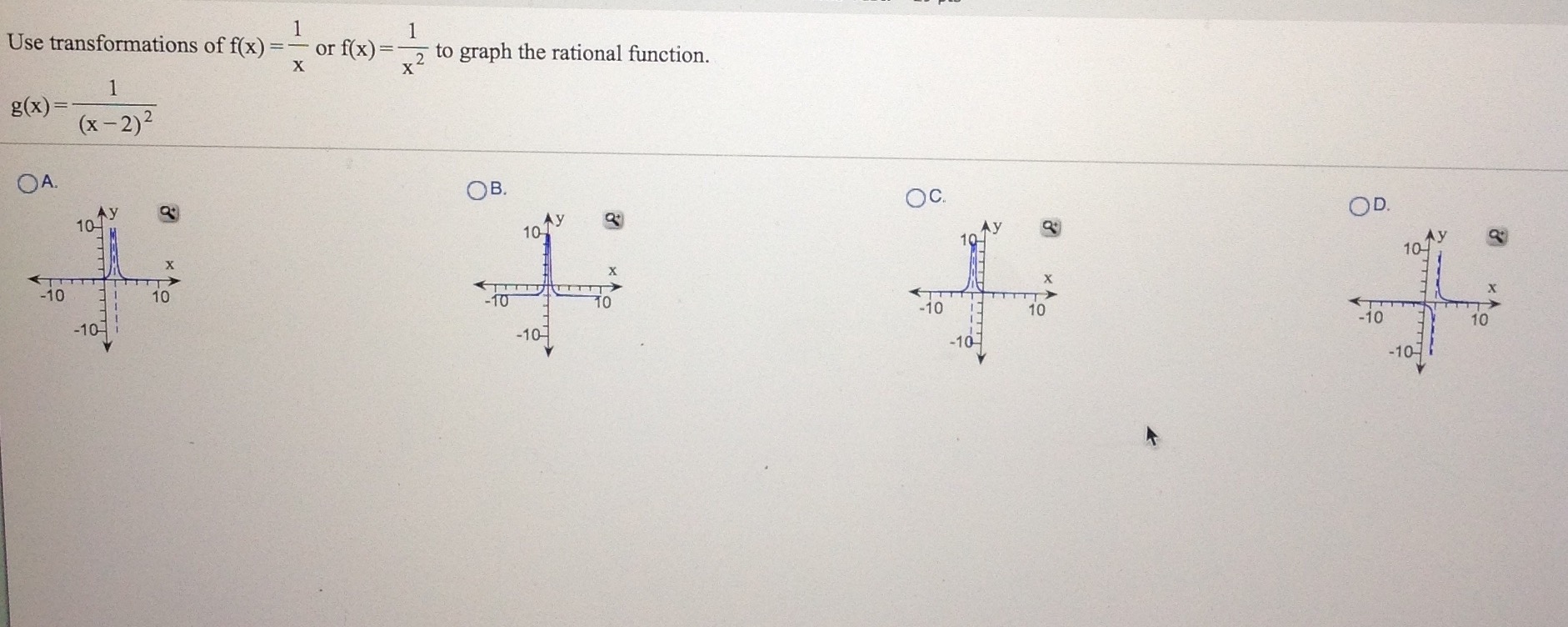



Solved Use Transformations Of F X 1 X Or F X 1 X 2 Chegg Com
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us CreatorsA y transformation affects the y coordinates of a curve You can identify a y transformation as changes are made outside the brackets of y = f ( x) We examine y transformations first since they behave as expected Upward shift f ( x) → f ( x) 4, this is a y shift This does not affect x coordinates but all the y coordinates go up by 4The following general form outlines the possible transformations f(x) = a f b(x − h) k a > 1 → Vertical stretch by a factor of a The graph of f(x) = x3 was reflected in the yaxis, compressed vertically by a factor of and translated 4 units up and 6 units to the left What is the equation for the




Ppt Gcse F Unctions And Transformations Of Graphs Powerpoint Presentation Id 185
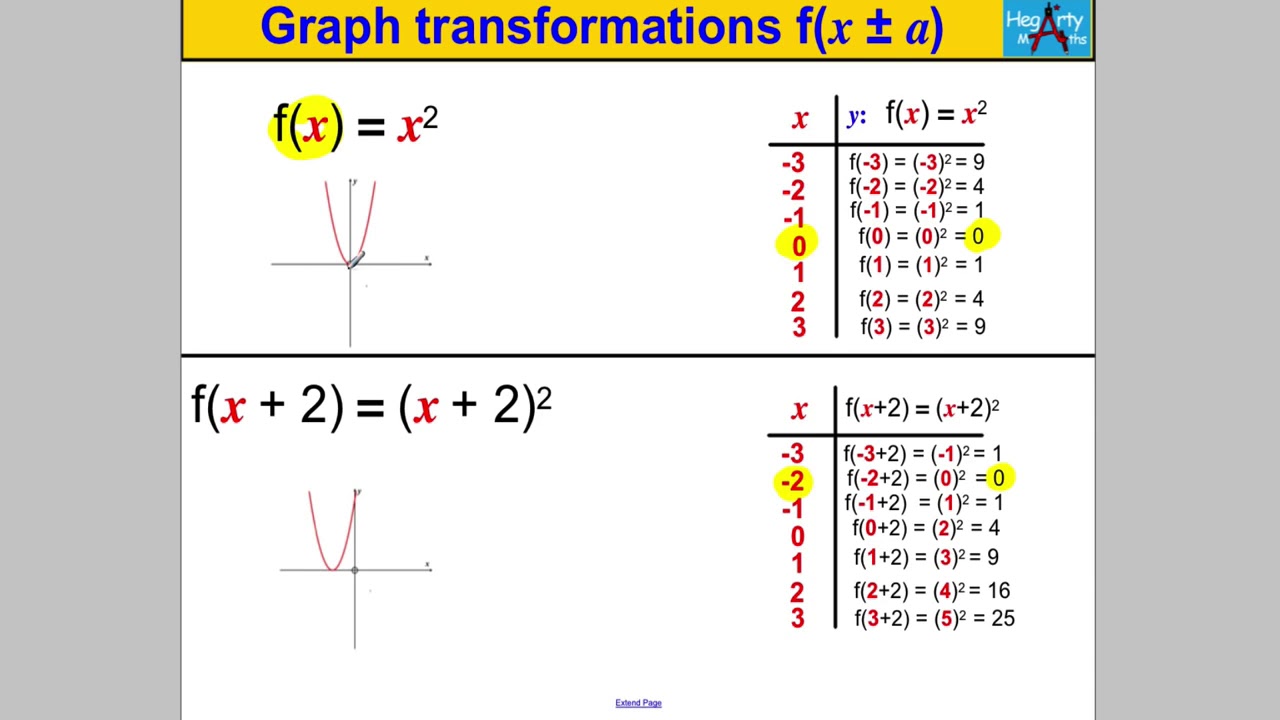



Graph Transformations 2 Fx A Copy Youtube
It's been stretched parallel to the yaxis by a factor of 2 and finally f (2x) Taking the graph of f (x) = x^2 again, this would give us the graph (2x)^2 = 4x^2, which is compressed horizontally by a factor of a half In summary f (x) a is f (x) shifted vertically a units f (x – a) is f (x) shifted horizontally a unitsPurplemath There are two other transformations, but they're harder to "see" with any degree of accuracy The first of these transformation is multiplication on the entire function To see what this looks like, compare the graphs of 2 × f (x) = 2x2, f (x) = x2, and ½ × f (x) = (½) x2, below graph of 2 × f (x) = 2x2 (This is skinnier · The basic shape will remain the same Multiplying a function by a negative constant, − f(x), reflects its graph in the x axis Multiplying the values in the domain by − 1 before applying the function, f( − x), reflects the graph about the y axis When




Quiz Transformations Of Parent Graphs Worksheet
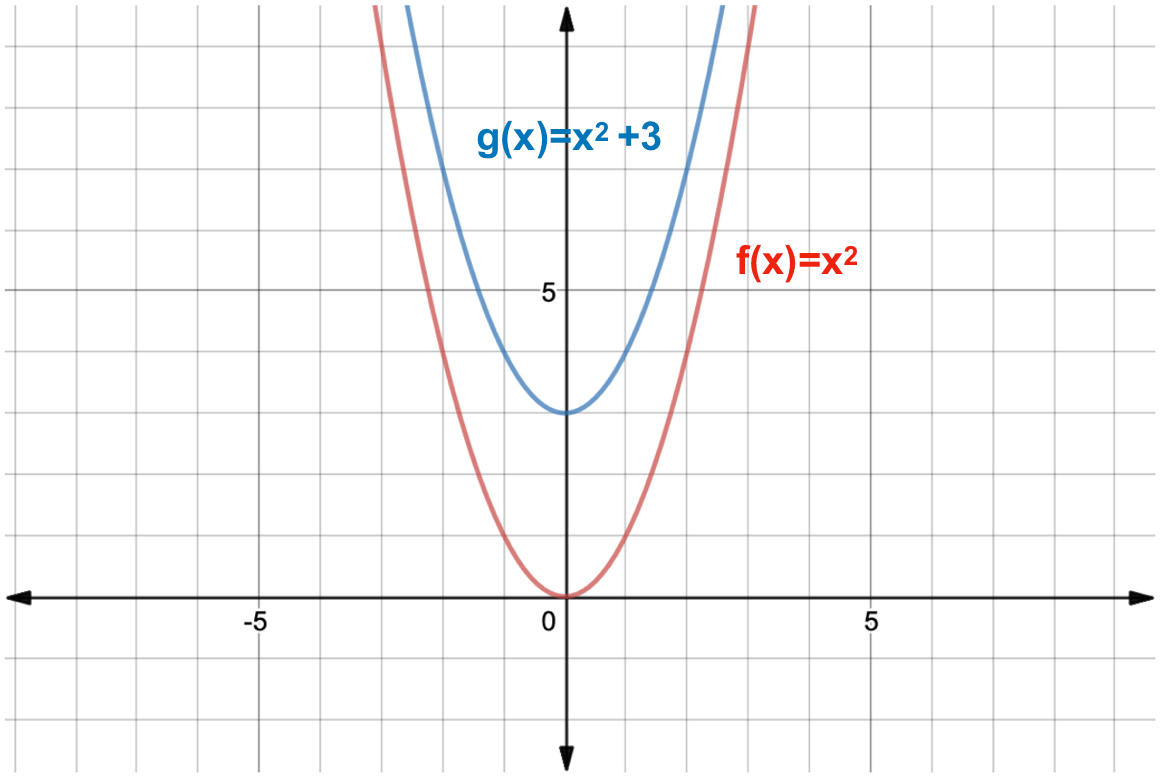



What Is A Function Transformation Expii
Dilation Dilation is also a transformation which causes the curve stretches (expands) or compresses (contracts) Multiplying a function by a positive constant vertically stretches or compresses its graph;The graph of the new function is easy to describe just take every point in the graph of f(x), and move it up a distance of d That is, if (a,b)isapointinthegraphoff(x), then (a,b d)isapointinthe graph of f(x)d As an explanation for what's written above If (a,b)isapointinthegraph of f(x), then that means f(a)=b · So, for any given y value, the x value that gets you there is moved 5 units to the negative side of the graph, which is left These two simple transformations up
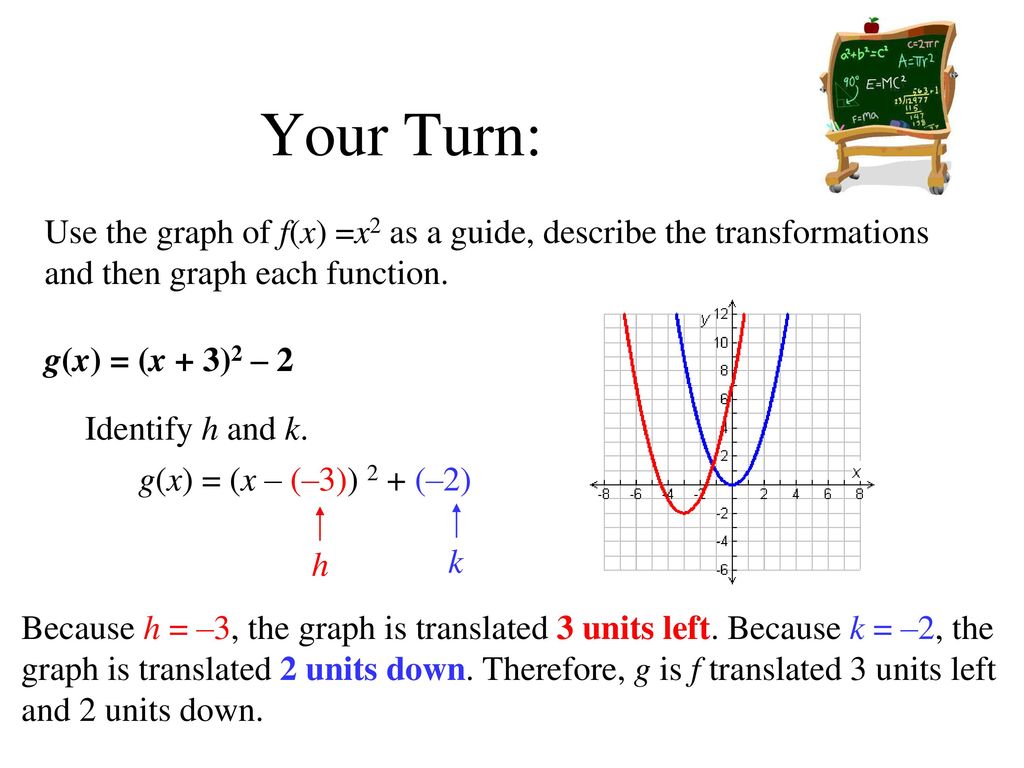



Quadratic Functions And Transformations Lesson Ppt Download
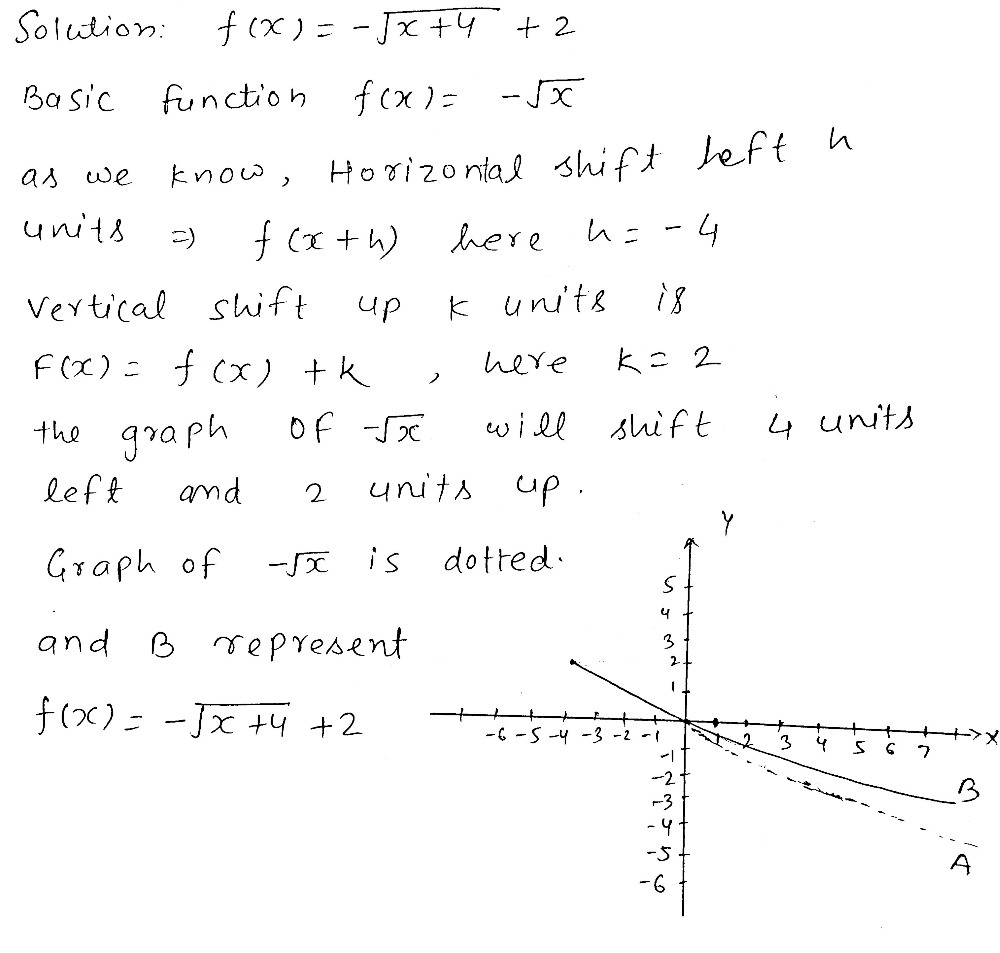



C2s1qwsfo5r4lm
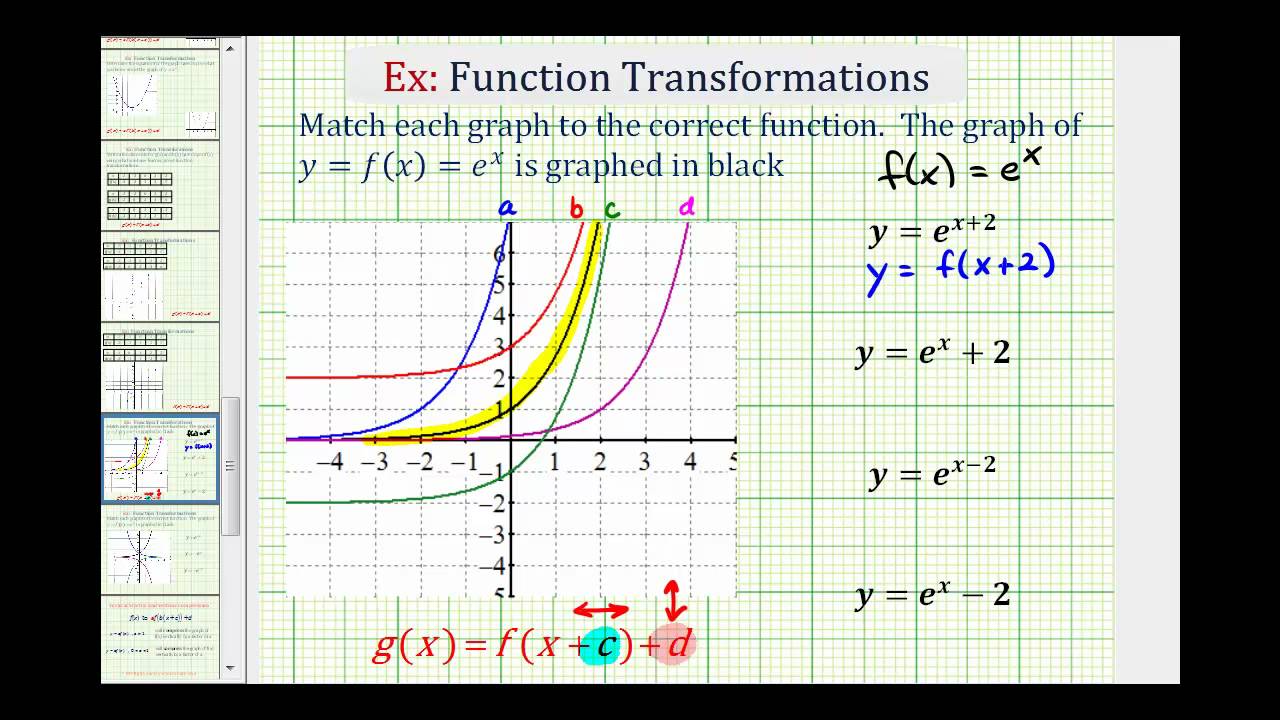



Horizontal And Vertical Translations Of Exponential Functions College Algebra
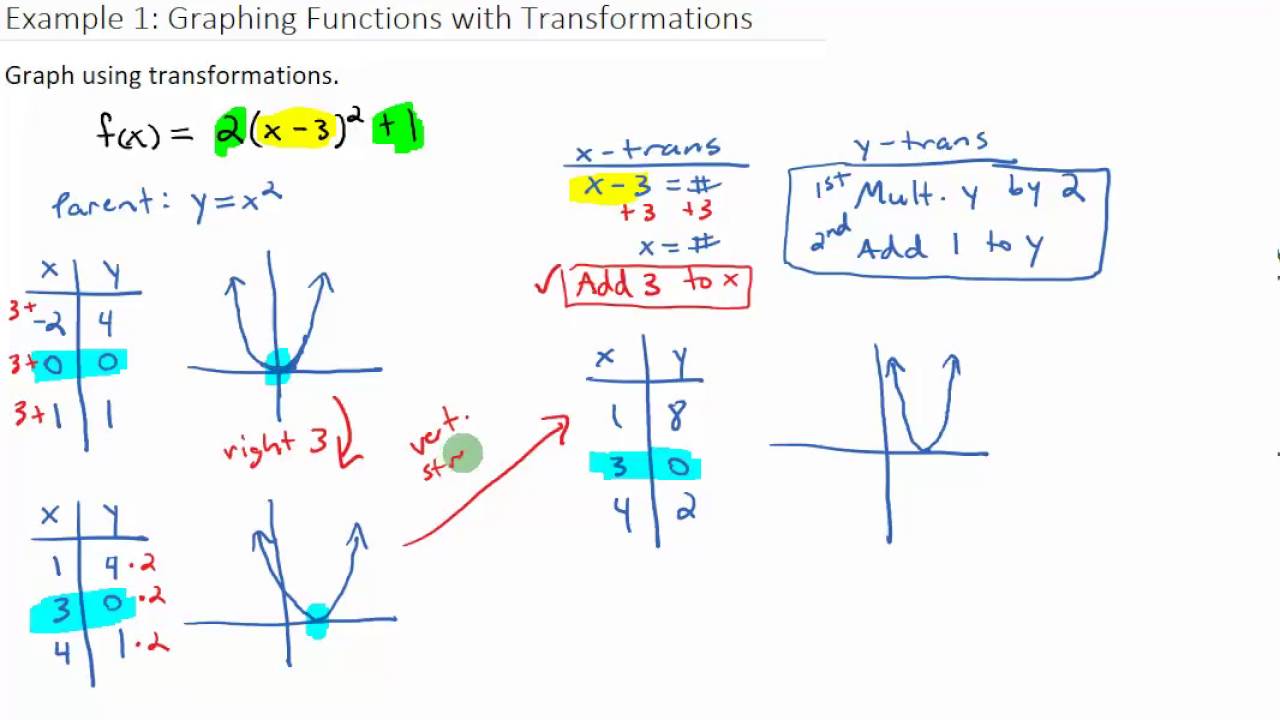



Example 1 Graphing A Function With Transformations Youtube



The Graph Of The F X Is Show Below Graph Each Transformed Function And List In Words The Transformation Used Socratic
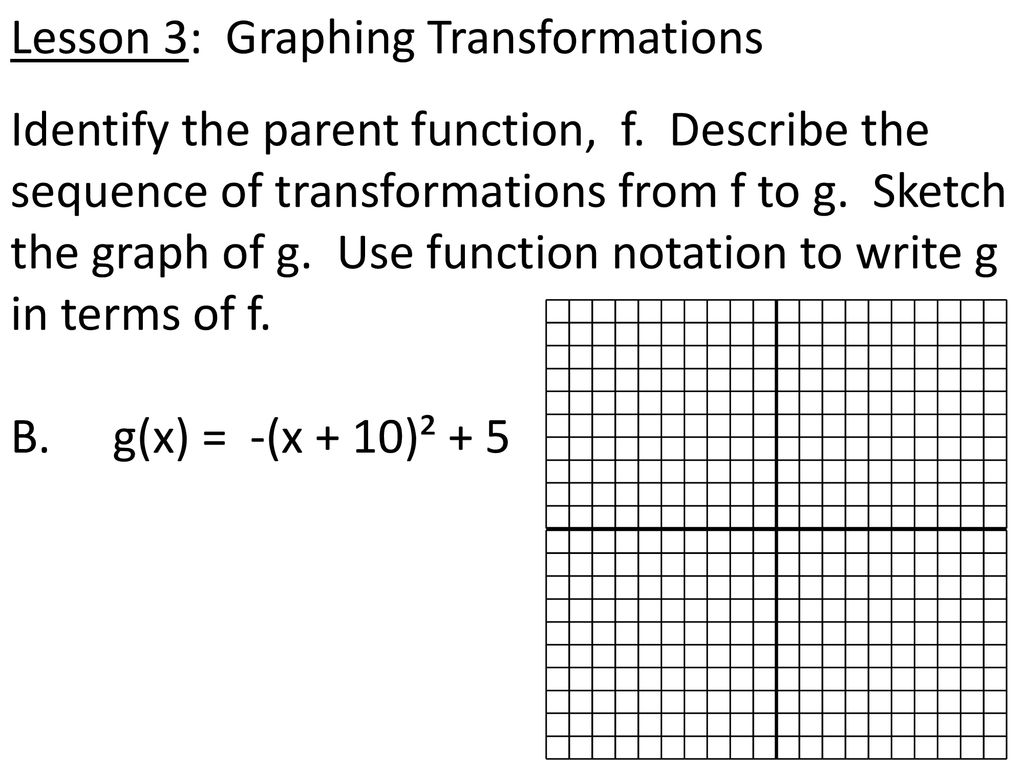



1 7 Notes Transformations Of Functions Ppt Download



Begin By Graphing F X 2 2 Then Use Transformations Of This Graph To Graph T Plainmath
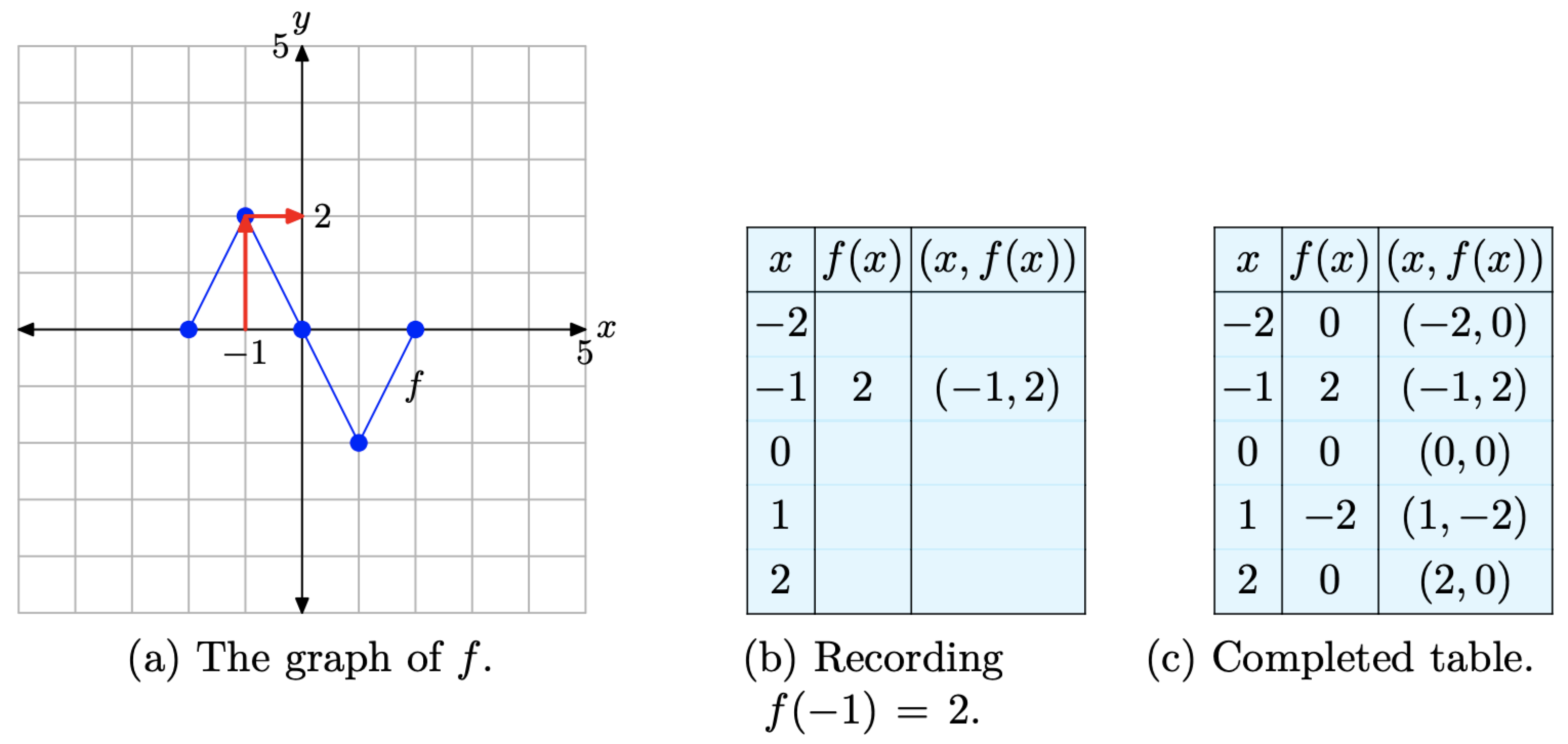



16 5 1 Vertical Transformations Mathematics Libretexts
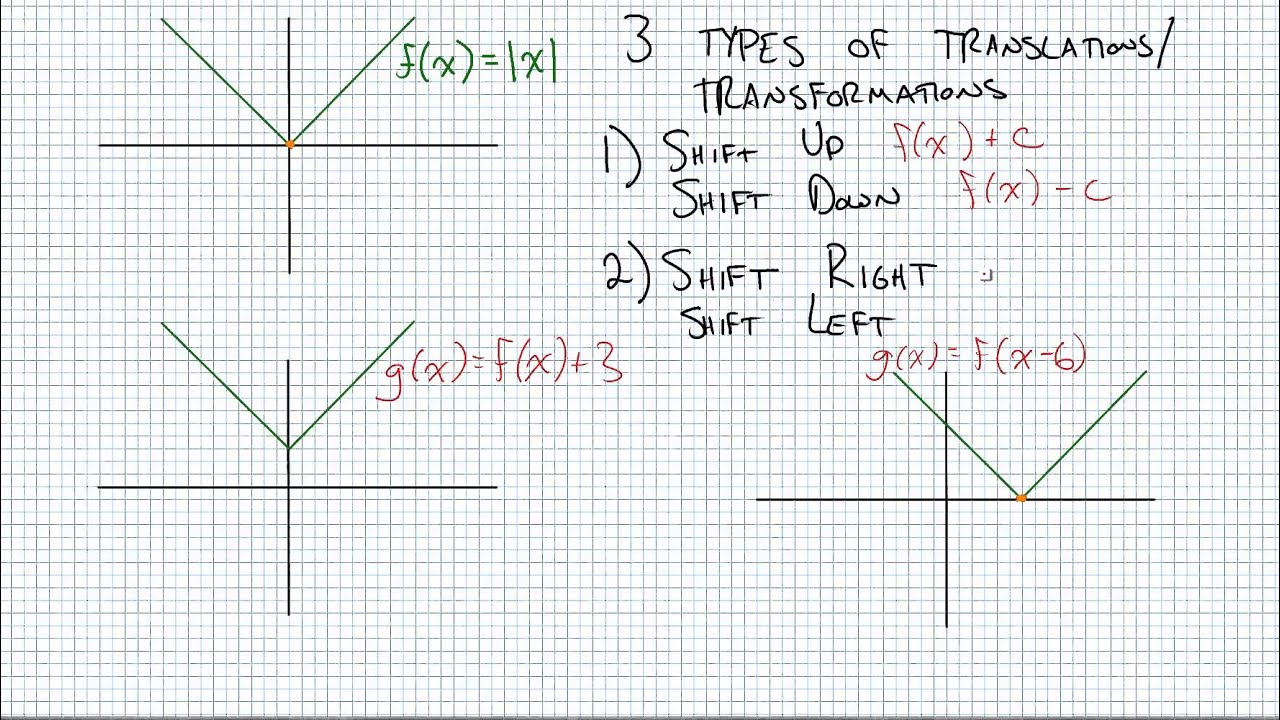



Section 1 8 Graph Transformation Rules Youtube




Transformation Of Graphs Maths Numeracy Educational School Posters




The Graph Of F X 2 X Is Shown In Black K Match Each Transformation Of This Function With A Graph Brainly Com




Transformations Of Functions Definitions Facts And Solved Examples Cuemath
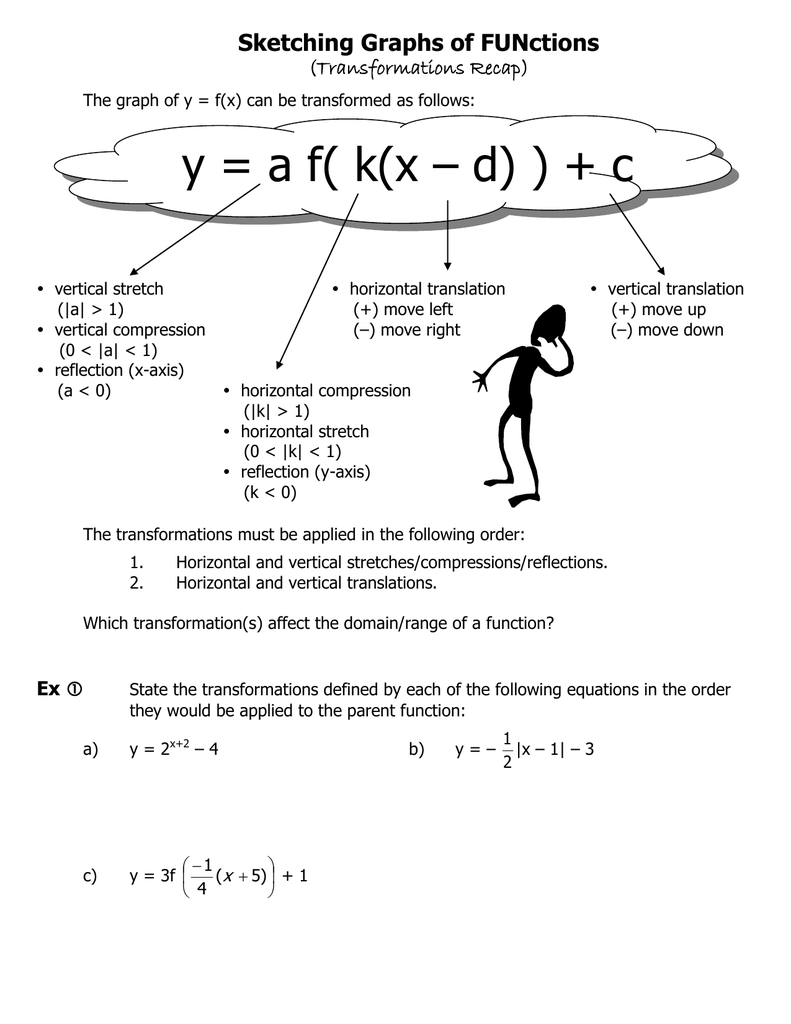



Y A F K X D C




Transforming Graphs Of Modulus Functions Youtube




Daily Warm Up Graph The Following Functions By Making A Table X Ppt Download
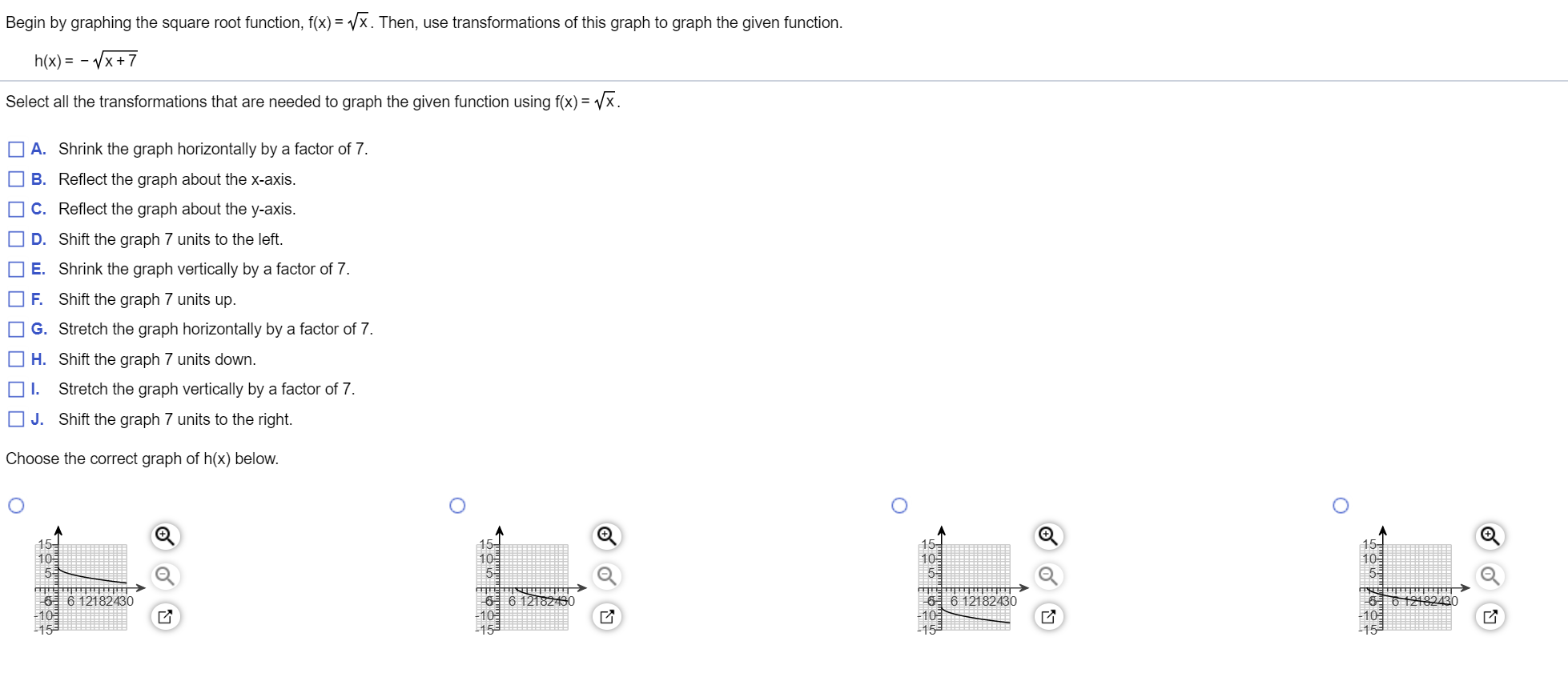



Begin By Graphing The Square Root Function F X Chegg Com




Answered 1 The Graph Of F X Is Given Below Bartleby




1 1 19 3 7 2 3 5 1 4 7 The Graph Above Is A Chegg Com




Begin By Graphing F X 3 Then Use Transformations Of Chegg Com
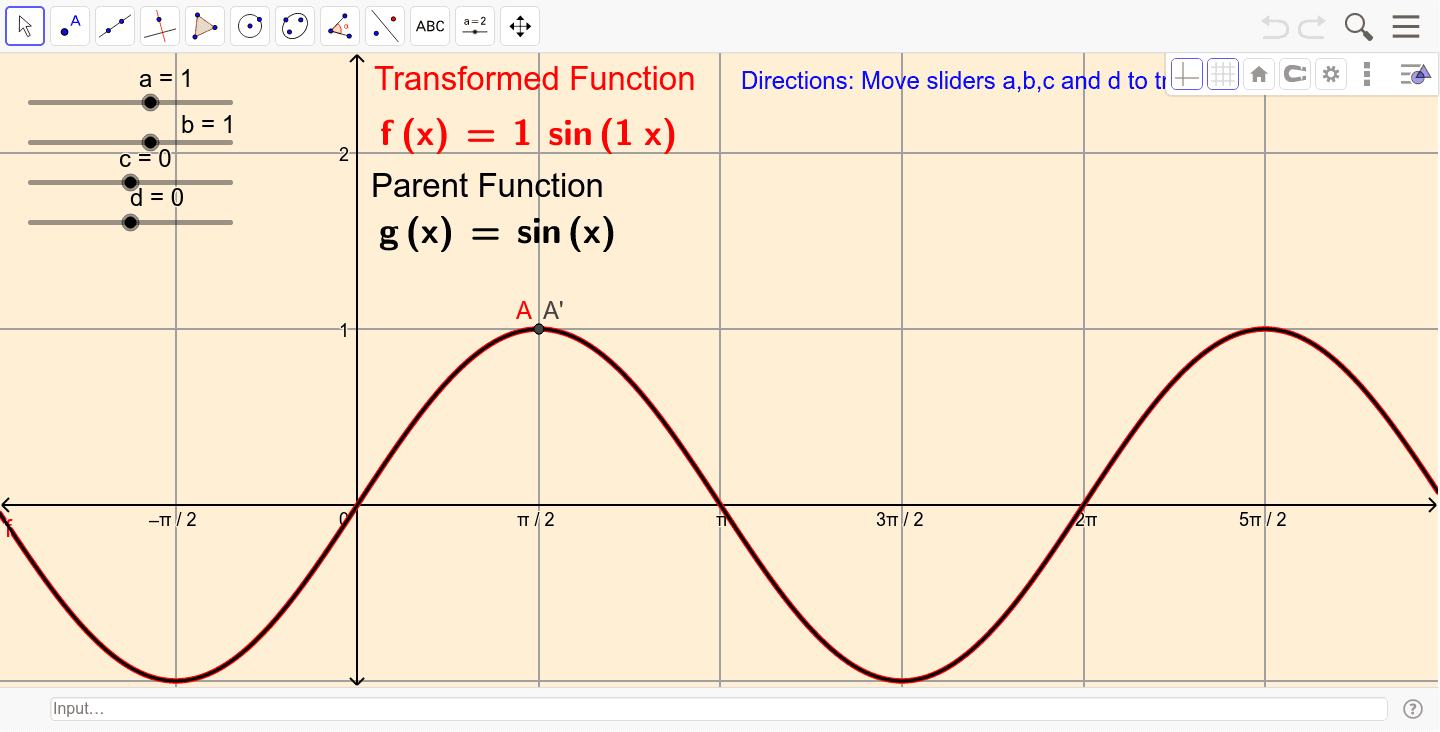



Transformations Of F X Sin X Geogebra




Pin On Best Teaching Resources Ever Bestresourceever
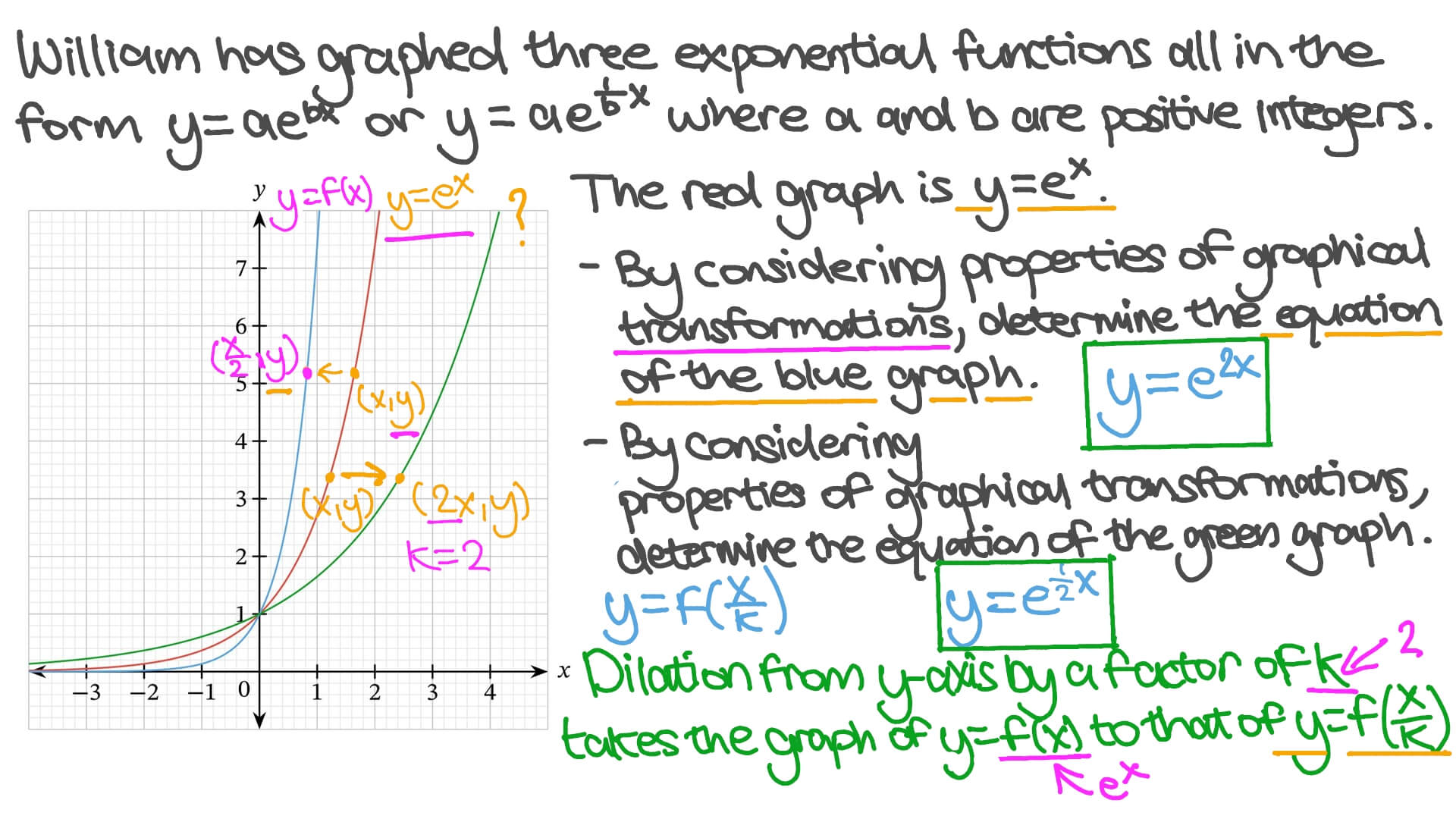



Question Video Graph Transformations Of Exponential Functions Nagwa




Finding The Equation Of A Transformation From The Graph Youtube
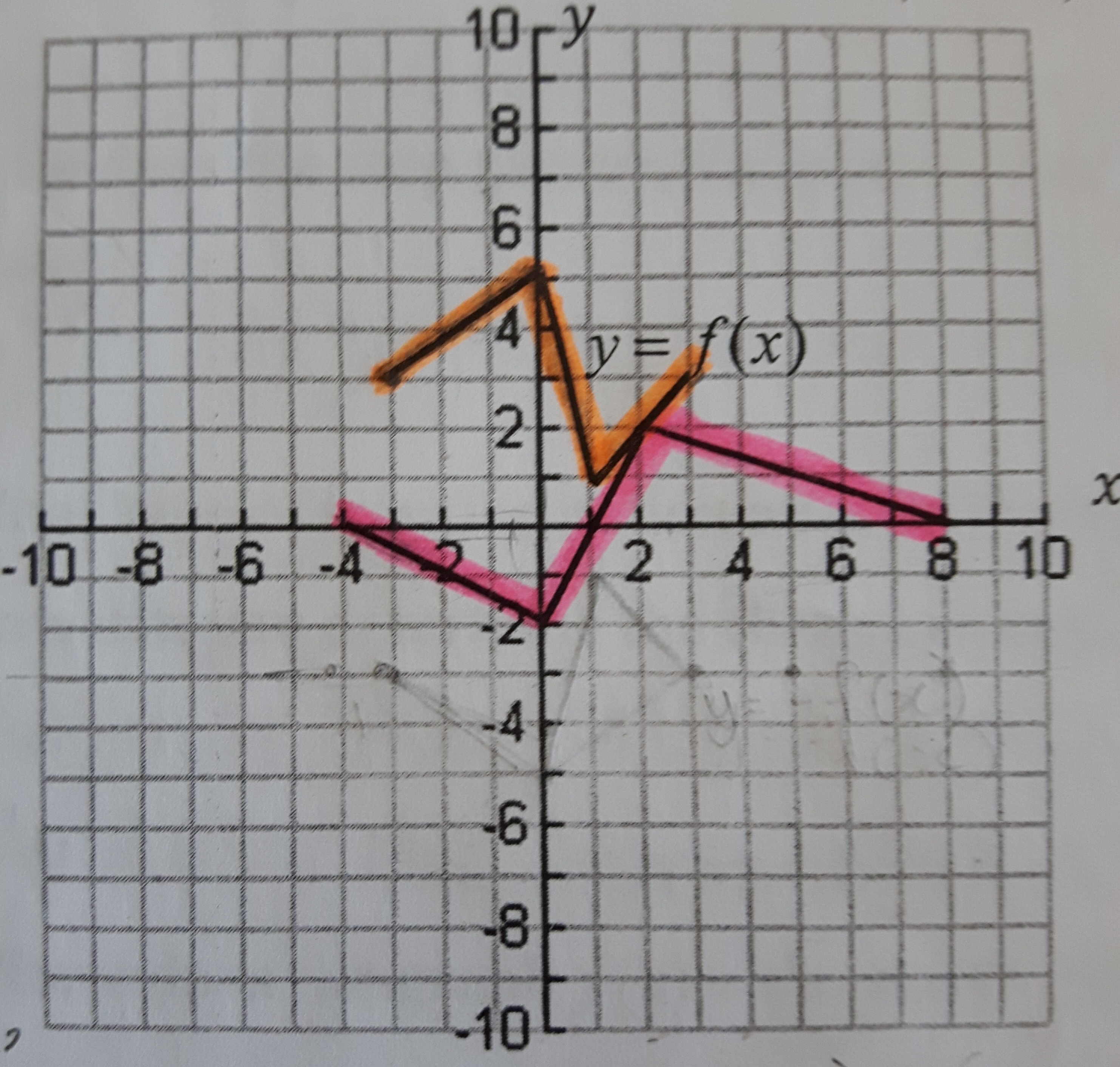



The Orange Graph Is The Function F X How Do You Describe The Transformations On The Pink Graph And Write An Equation For It Socratic
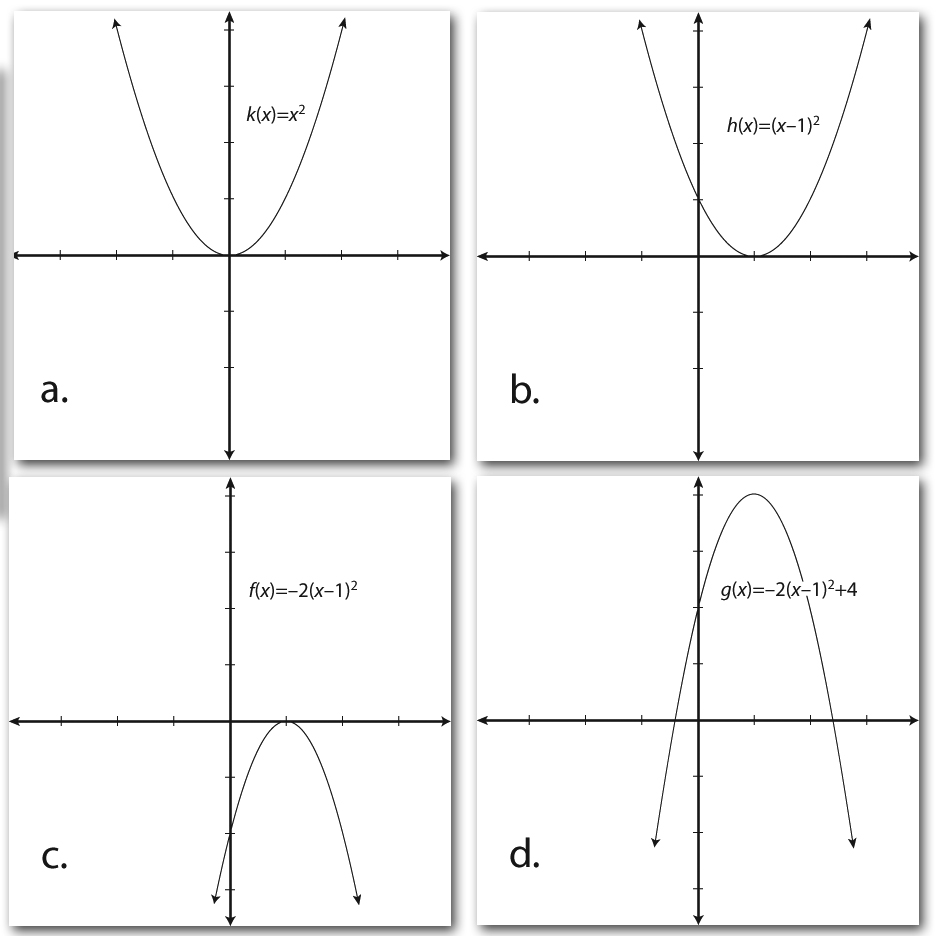



How To Combine Various Transformations Dummies




Mystery Transformation Reflections In The Why




Solved 7 Begin By Graphing F X 3 Then Use Transformati Chegg Com



Functions Graph Transformations Poster




Notes For Eer 4 Graph Transformations Vertical Horizontal Shifts Vertical Stretching Compression And Reflections Of Basic Functions Pdf Free Download
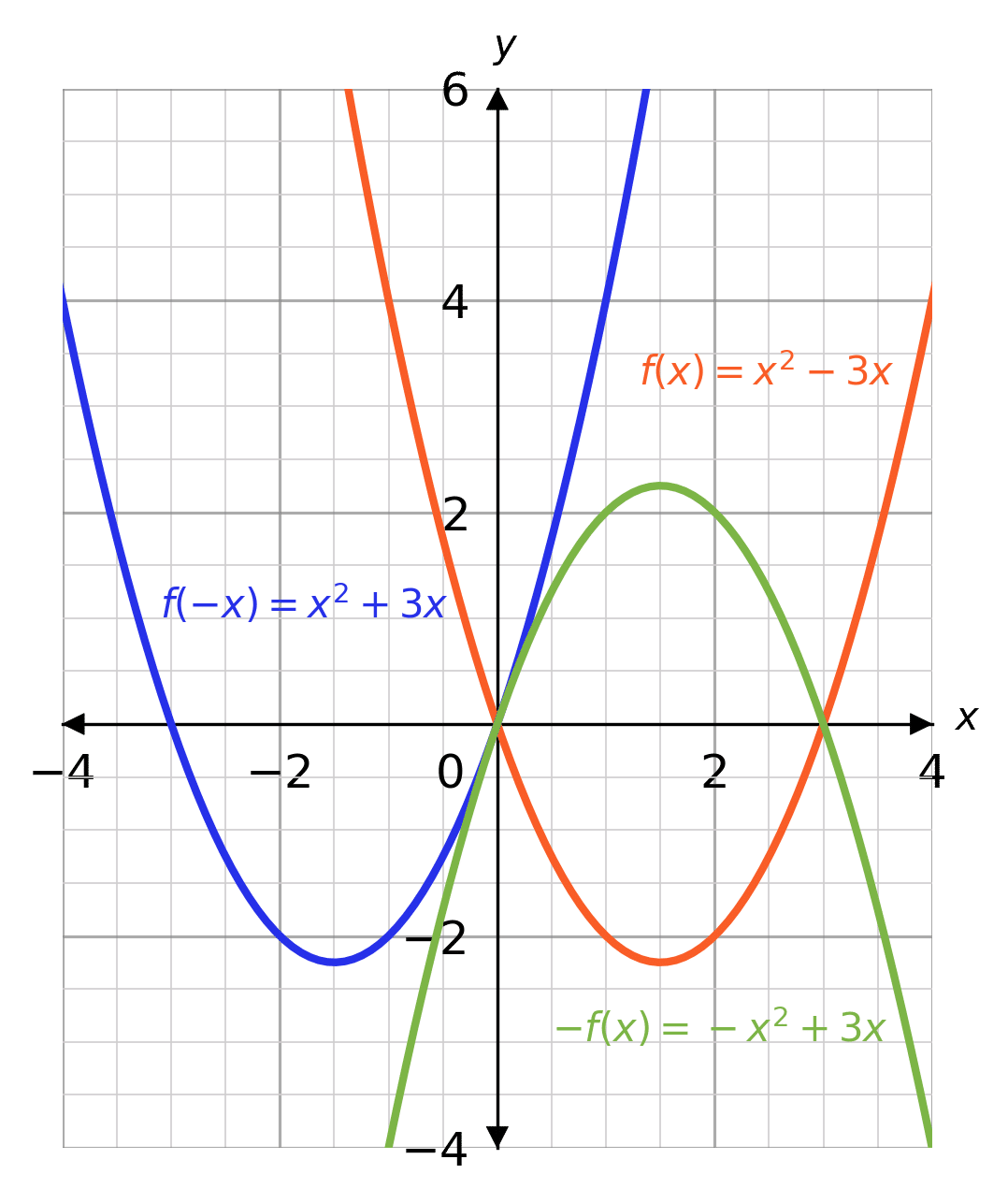



Graph Transformations Worksheets Questions And Revision Mme




Function Transformation Summary The Square Root Function Youtube




01 Transformations Of Graphs




Reflections Of Trig Graphs Examsolutions




Review Transformations Of Parent Graphs Worksheet




Pin On Best Teaching Resources Ever Bestresourceever




1 3 Combining Transformations Ppt Download
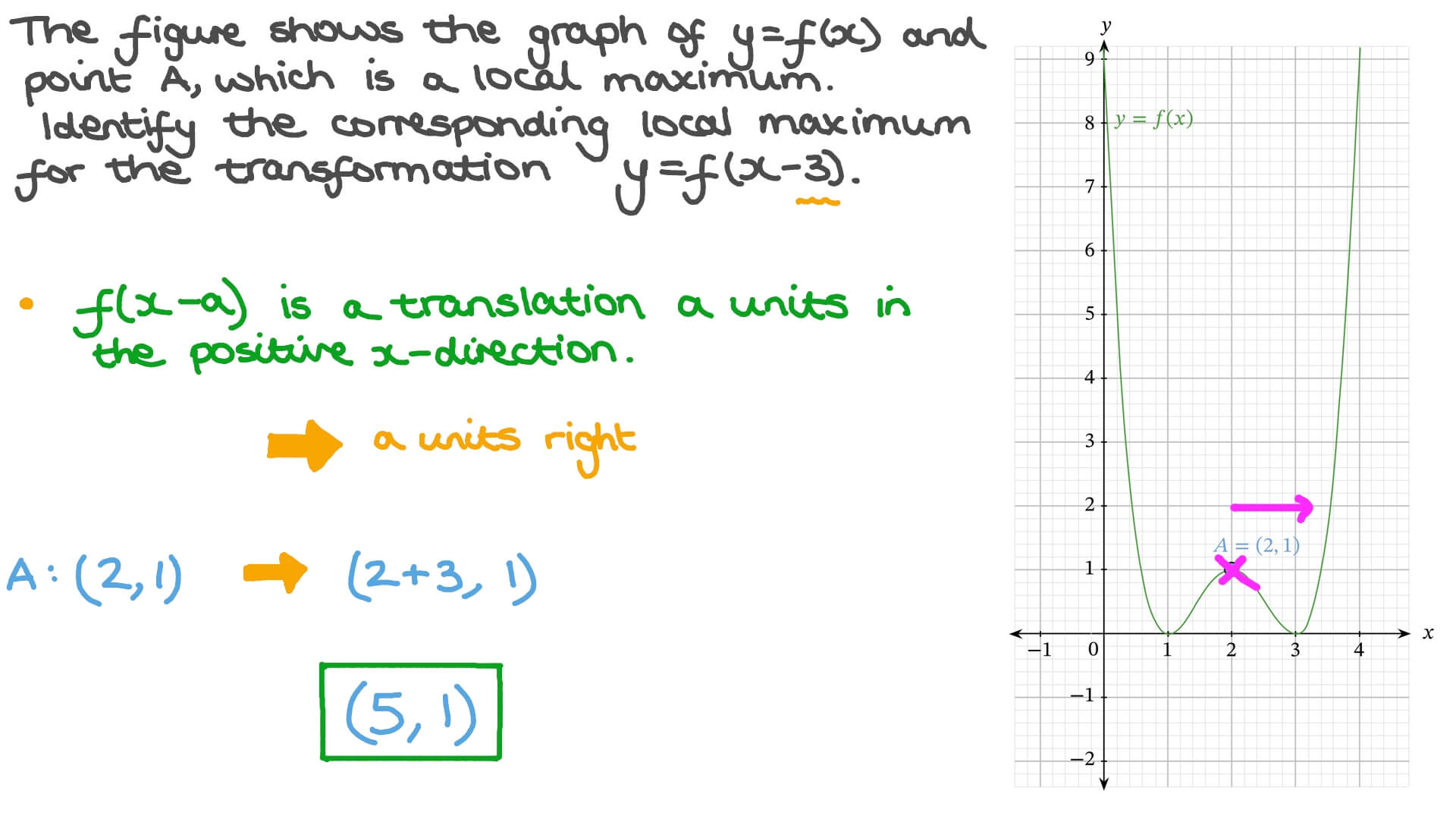



Question Video Identifying The Coordinates Of Points Following A Transformation Nagwa




Use The Graphs Of F And G To Describe The Transformation From The Graph F To The Graph G Brainly Com
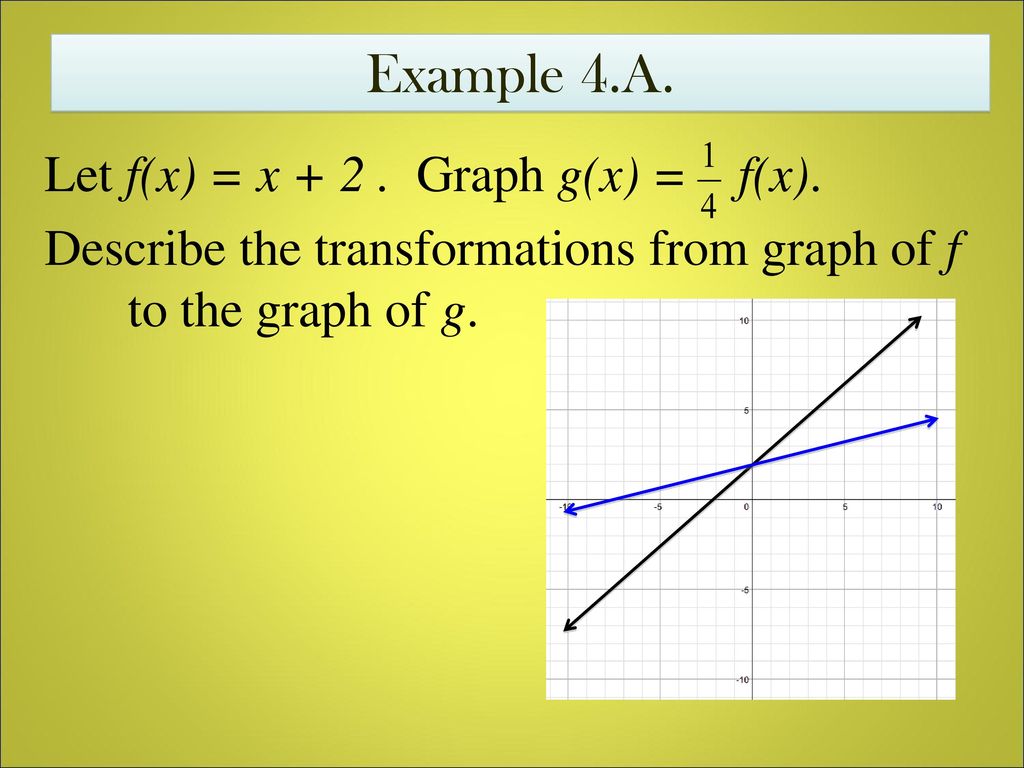



Daily Warm Up Match Each Function With Its Graph Ppt Download
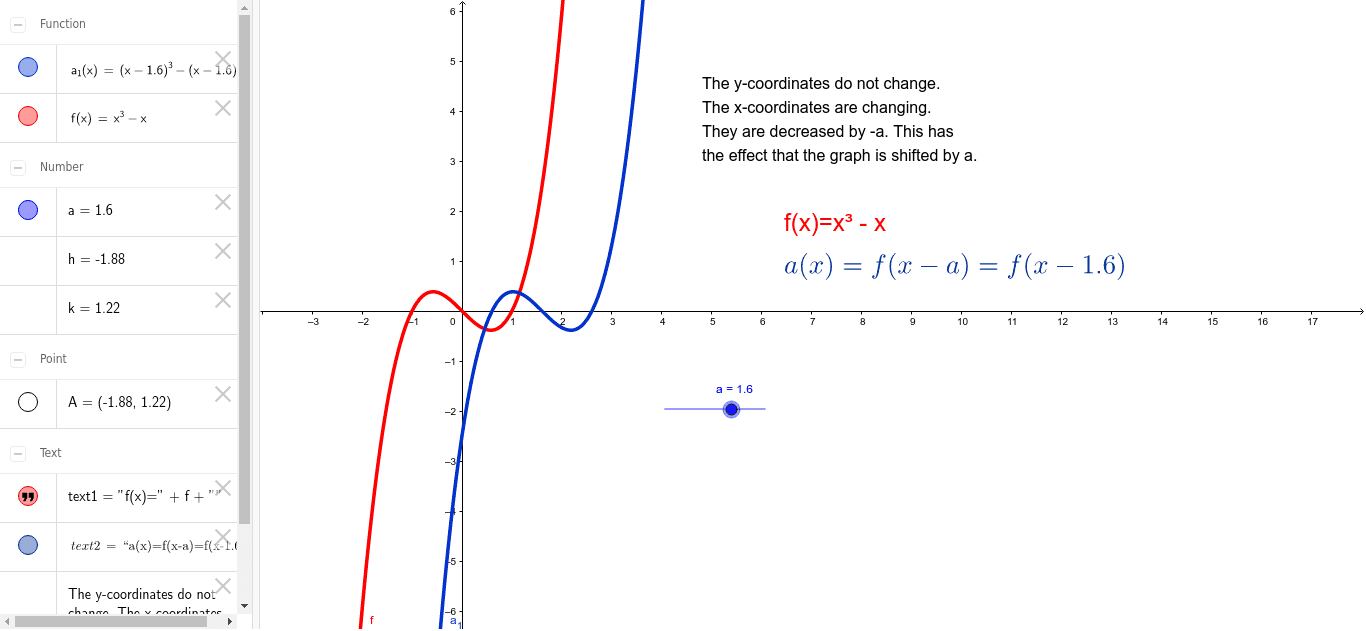



Kopiya Graph Transformations A1 X F X A By Nico Geogebra




Graphing Transformation Lab College Algebra Math 1050 Docsity
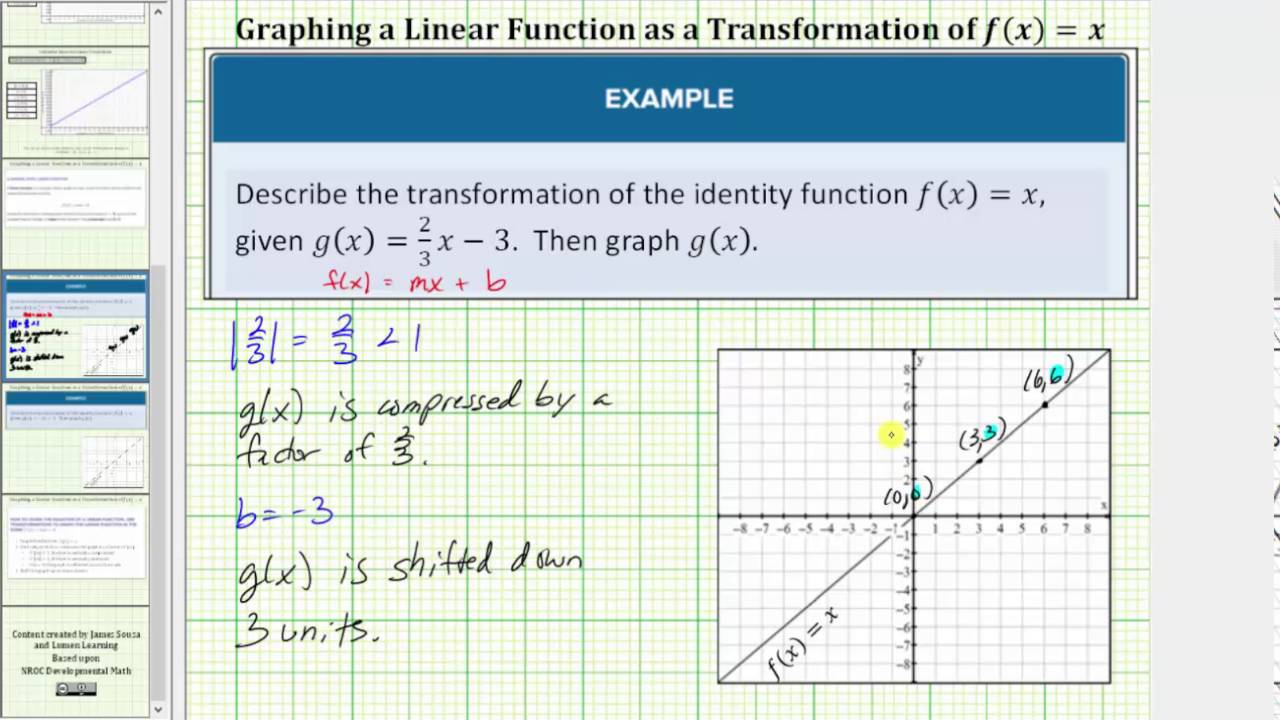



Graph A Linear Function As A Transformation Of F X X Youtube
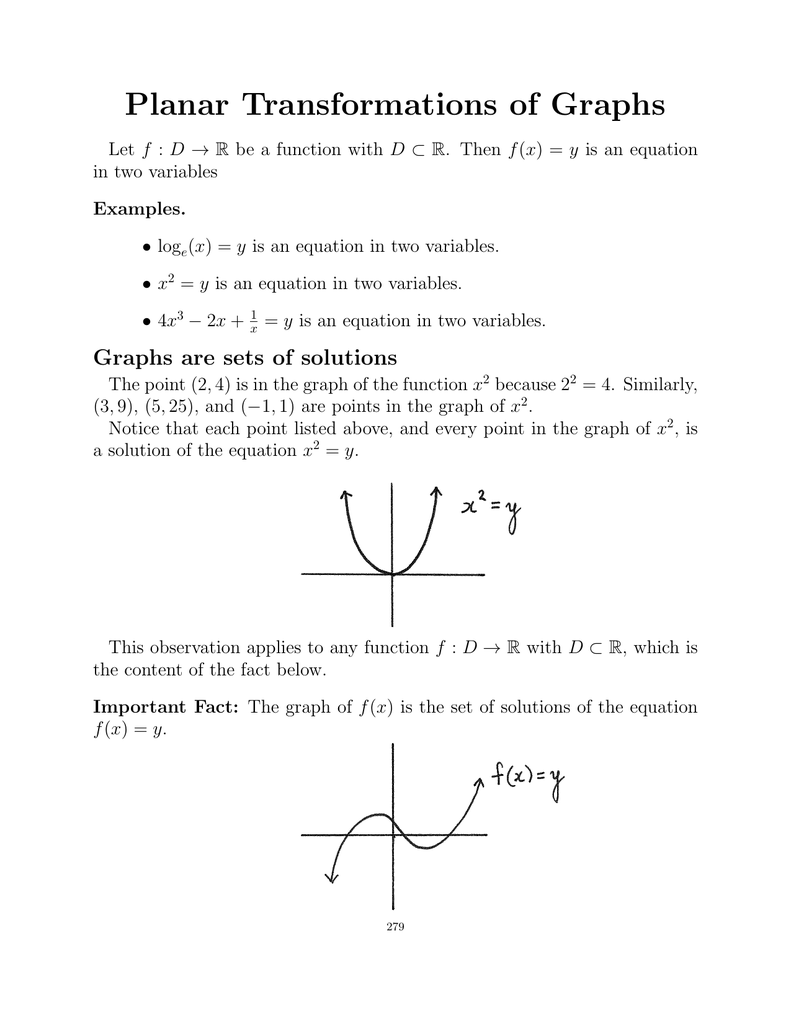



Planar Transformations Of Graphs F X F
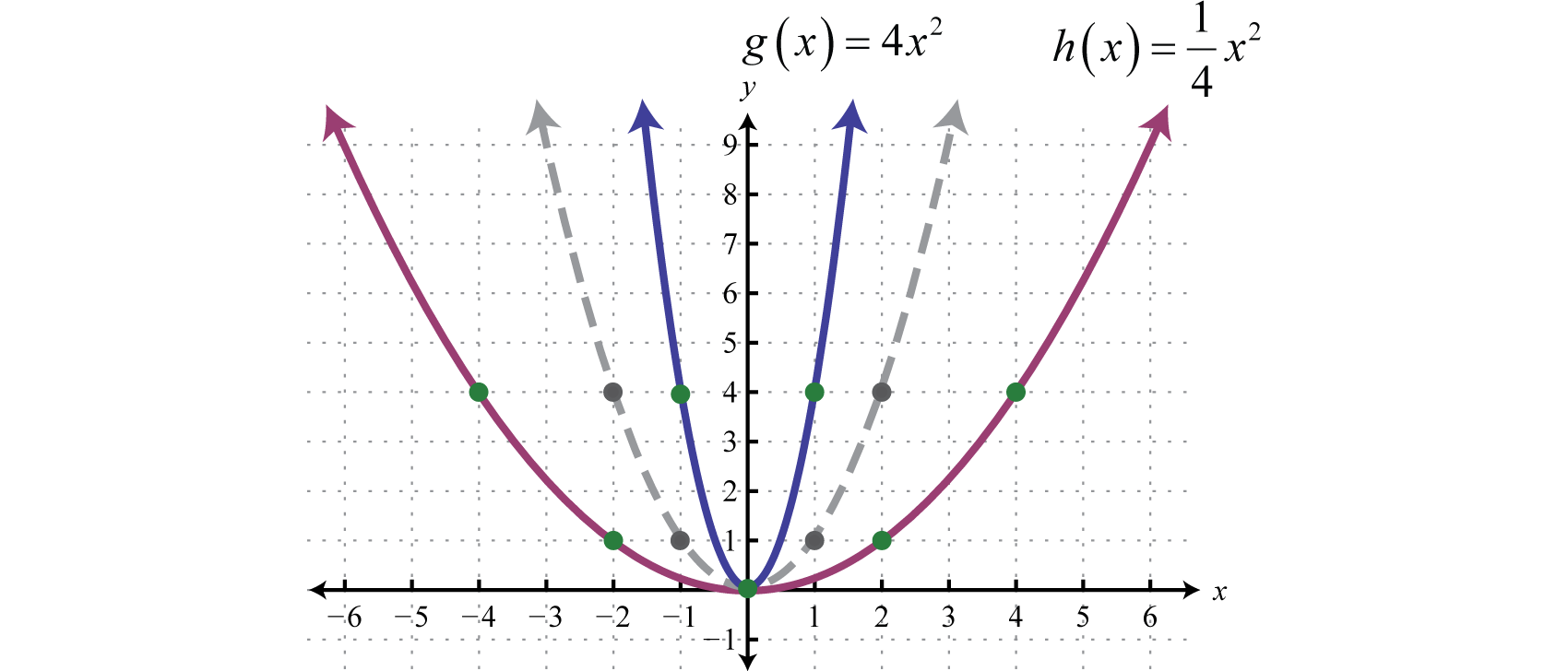



Using Transformations To Graph Functions




Function Transformation Video Lessons Examples And Solutions



Vce School Notes Graph Transformations
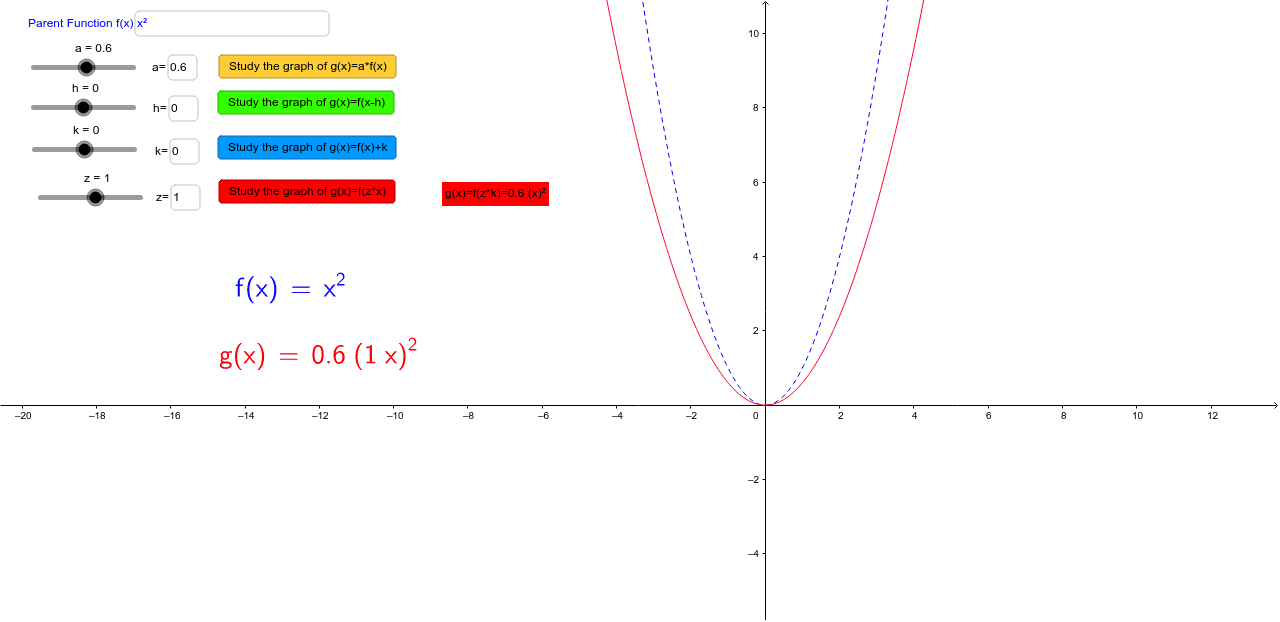



Graph Transformations Discovering Manipulating Functions Geogebra
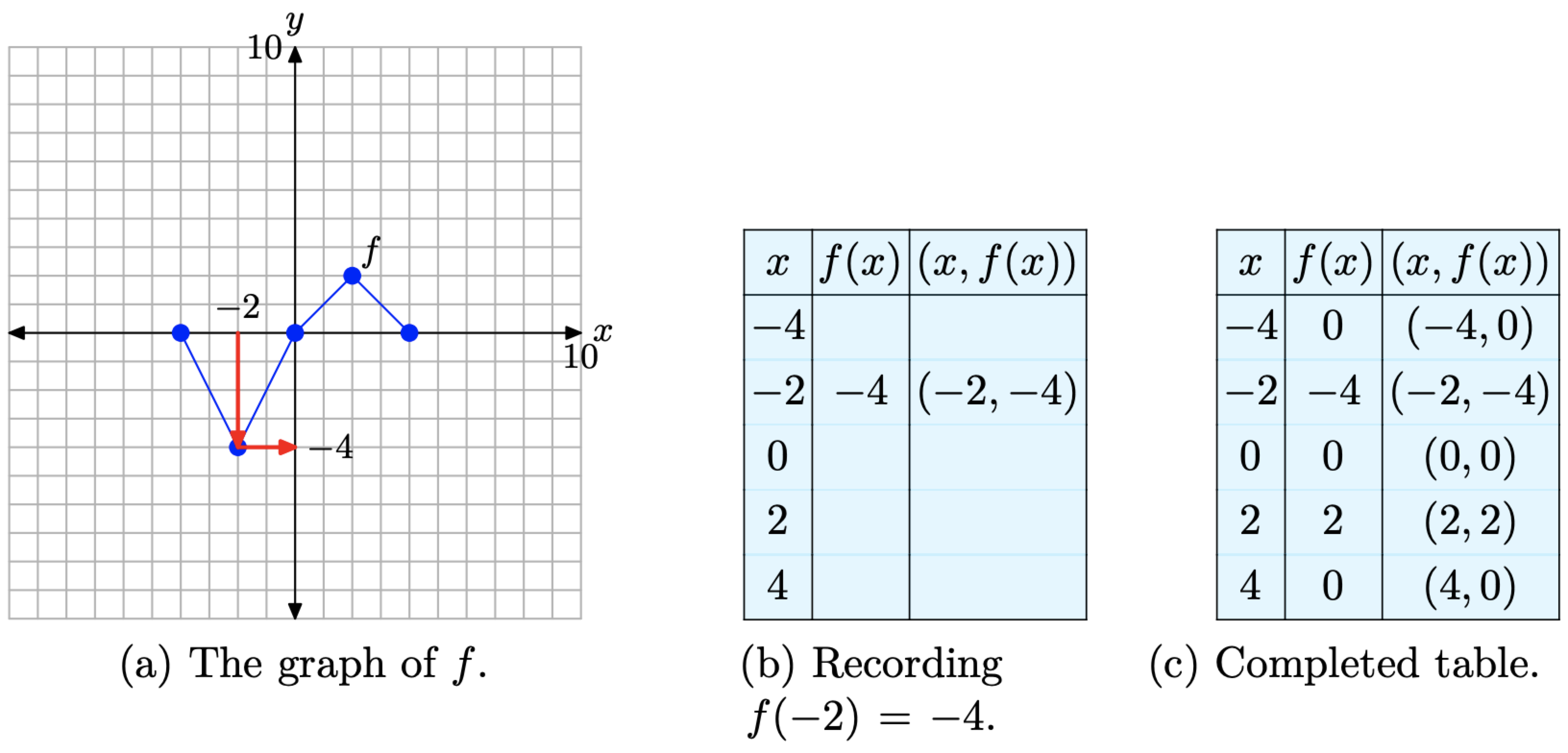



16 5 2 Horizontal Transformations Mathematics Libretexts
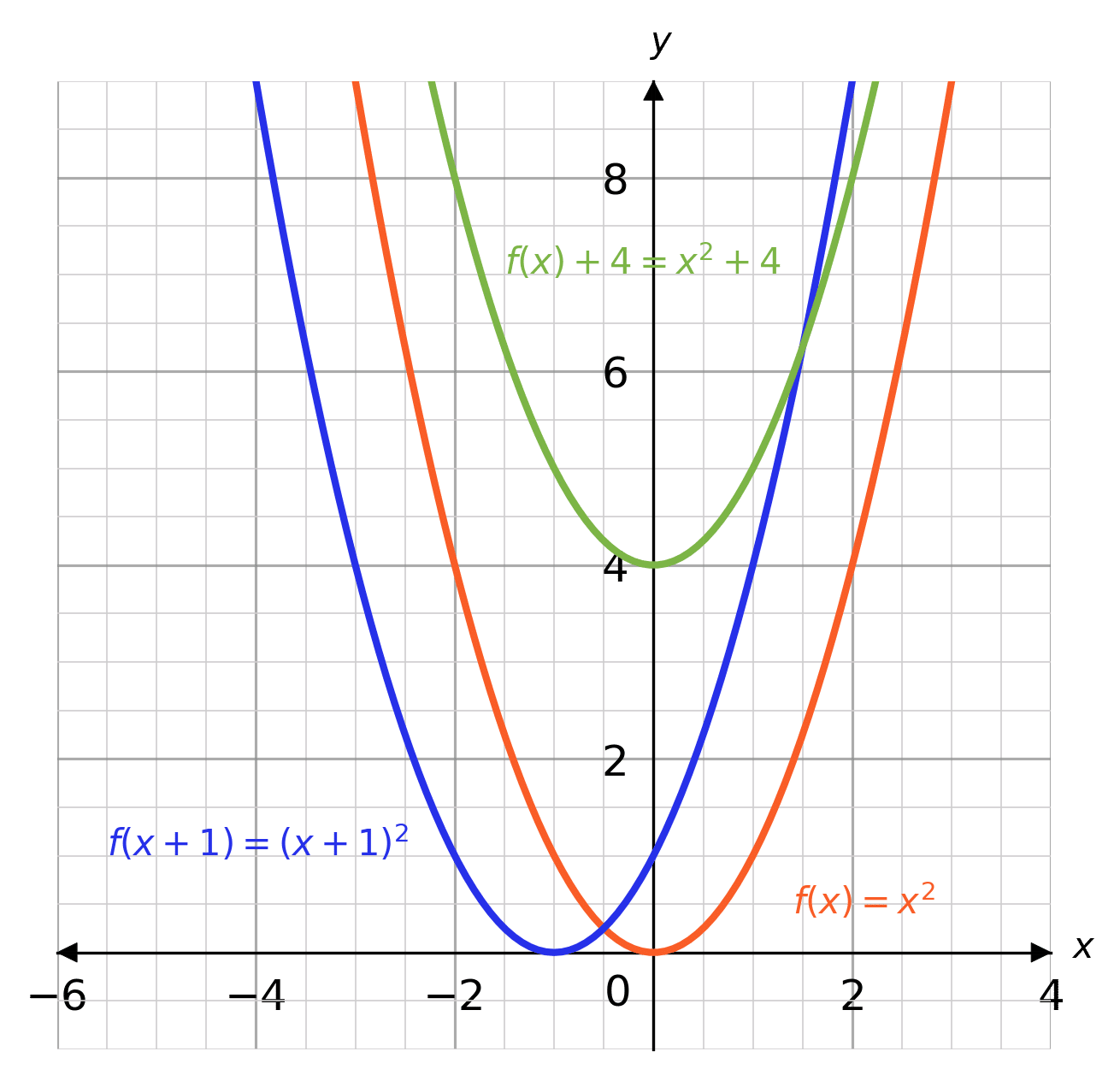



Graph Transformations Worksheets Questions And Revision Mme




12 Fx Graph Transformation រ បភ ពប ល ក Images




Using Transformations To Graph Functions
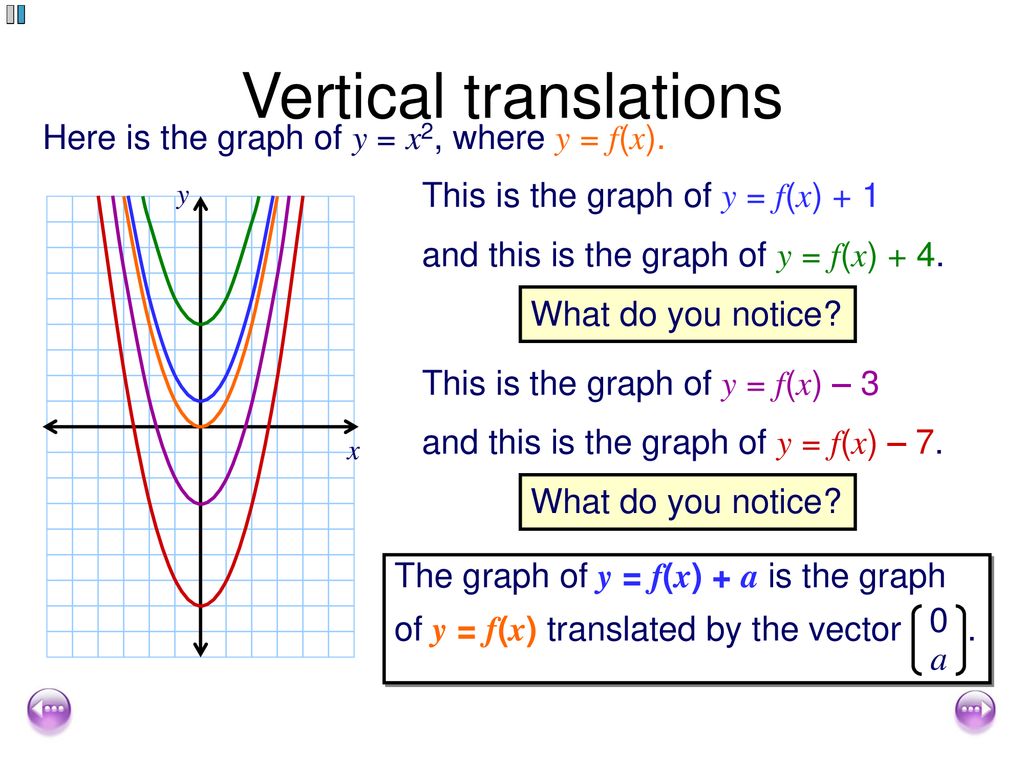



Transforming Graphs Of Functions Ppt Download




Function Transformations Horizontal And Vertical Stretches And Compressions Youtube




Graph Transformations Rules Google Search Teaching Algebra High School Math Activities Learning Mathematics



Solved Use Transformations Of F X To Graph G X 1 X X 6 3 Select The Correct Graph Av O C Ay Od Course Hero
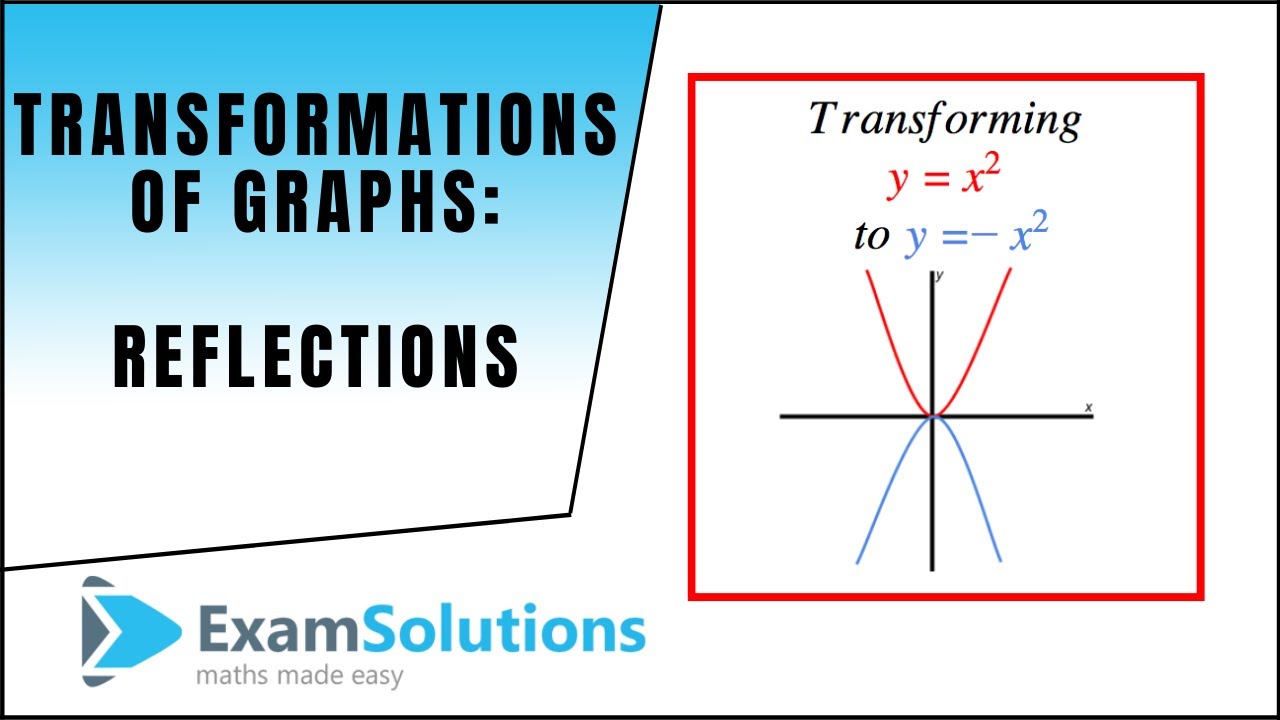



Transformations Of Graphs Reflections Y F X F X Examsolutions Youtube
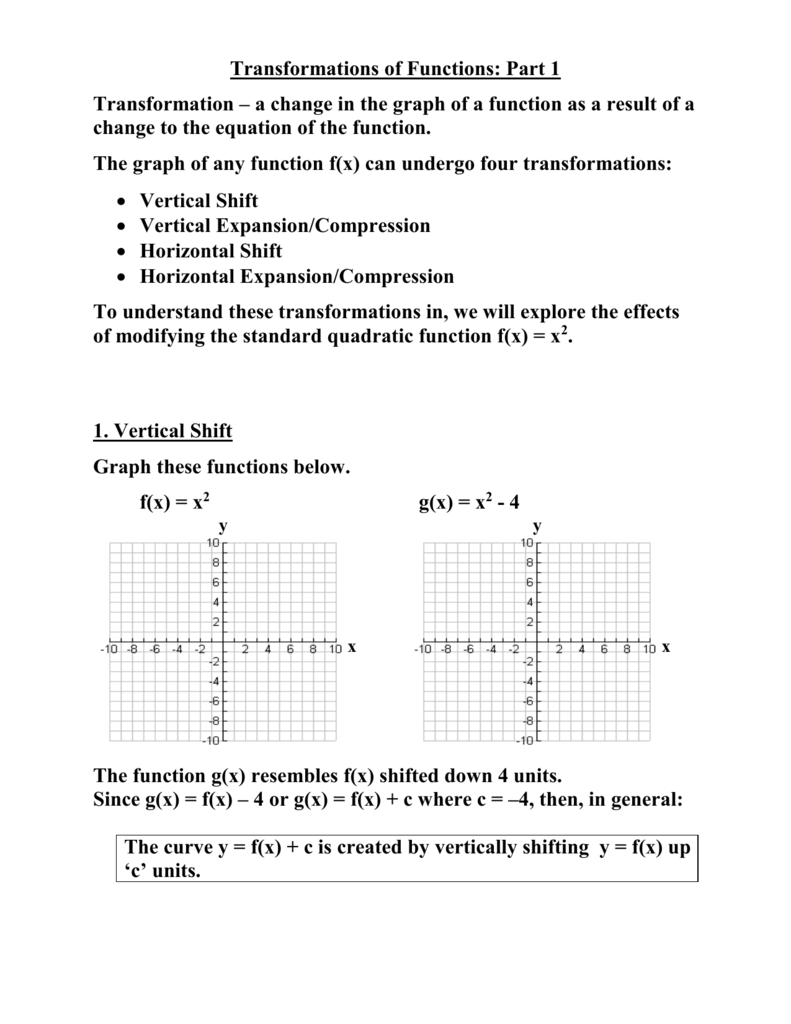



Transformations Of Functions Part 1
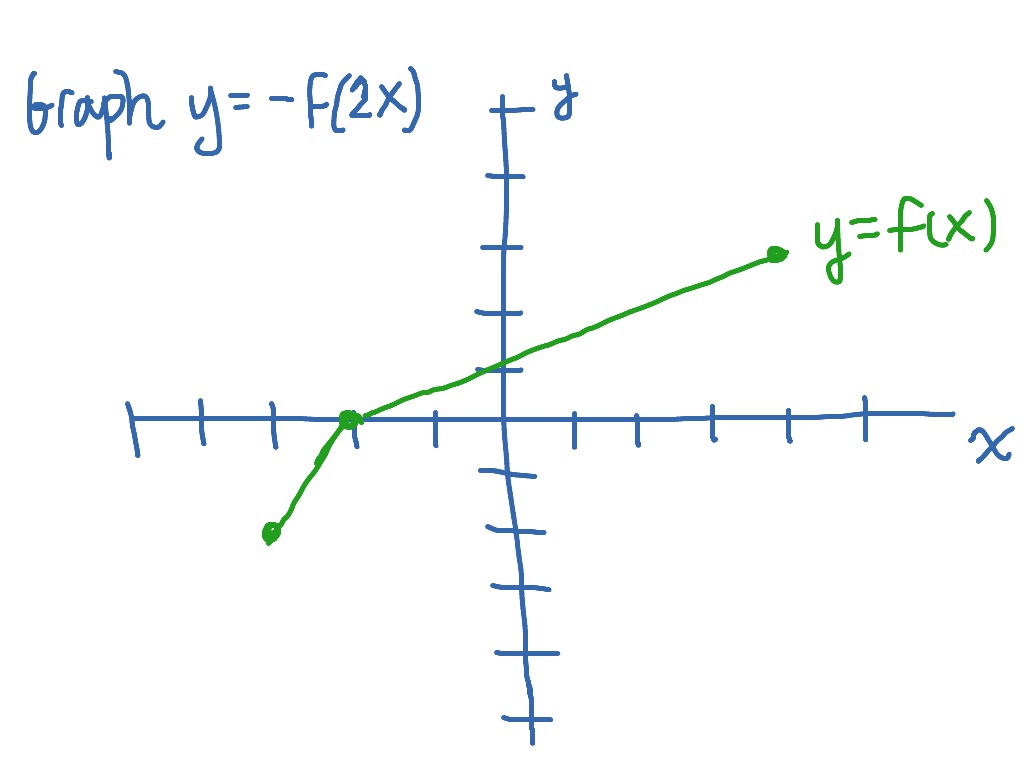



Graphing Y F 2x As A Transformation Of Y F X Math Showme
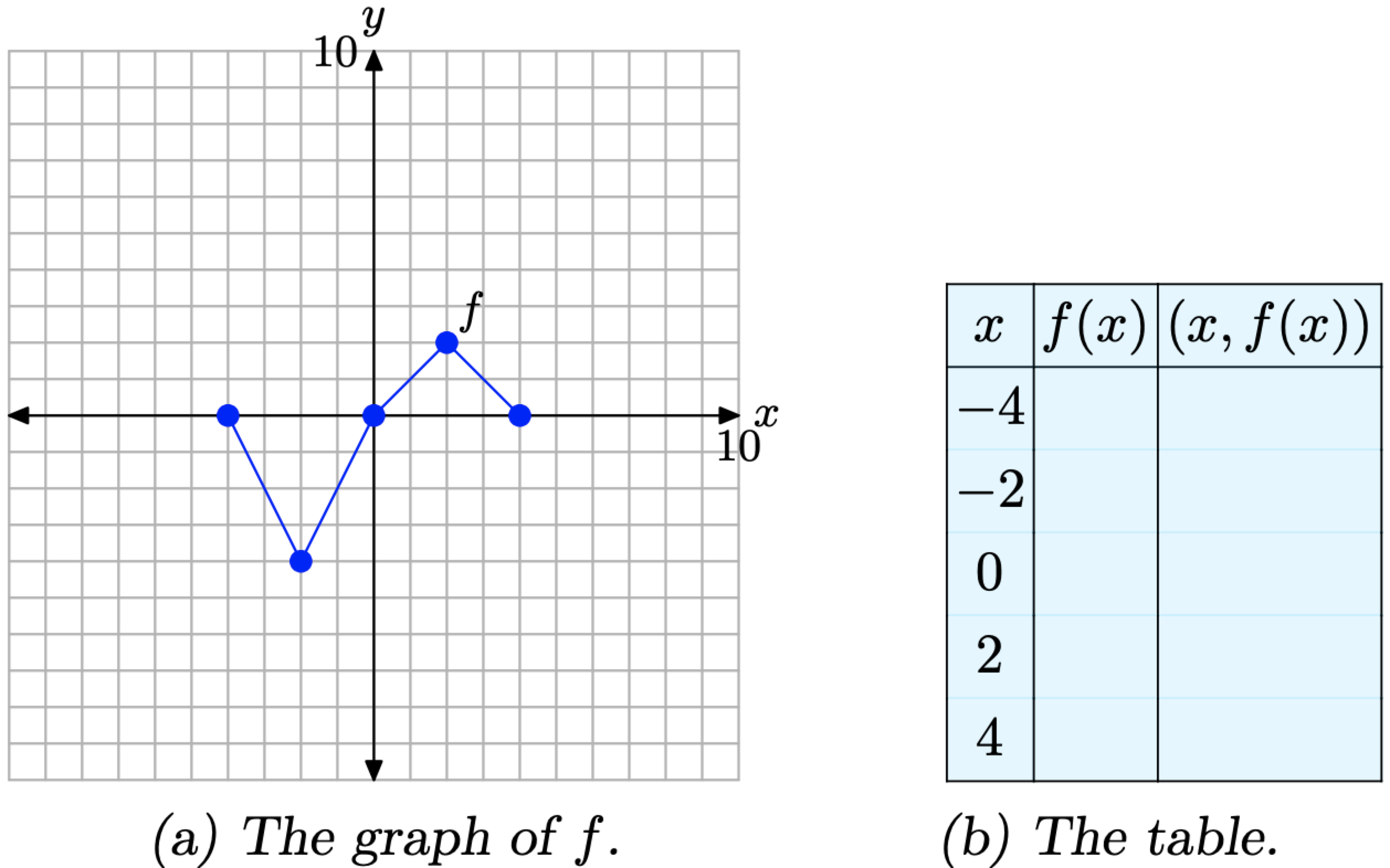



16 5 2 Horizontal Transformations Mathematics Libretexts
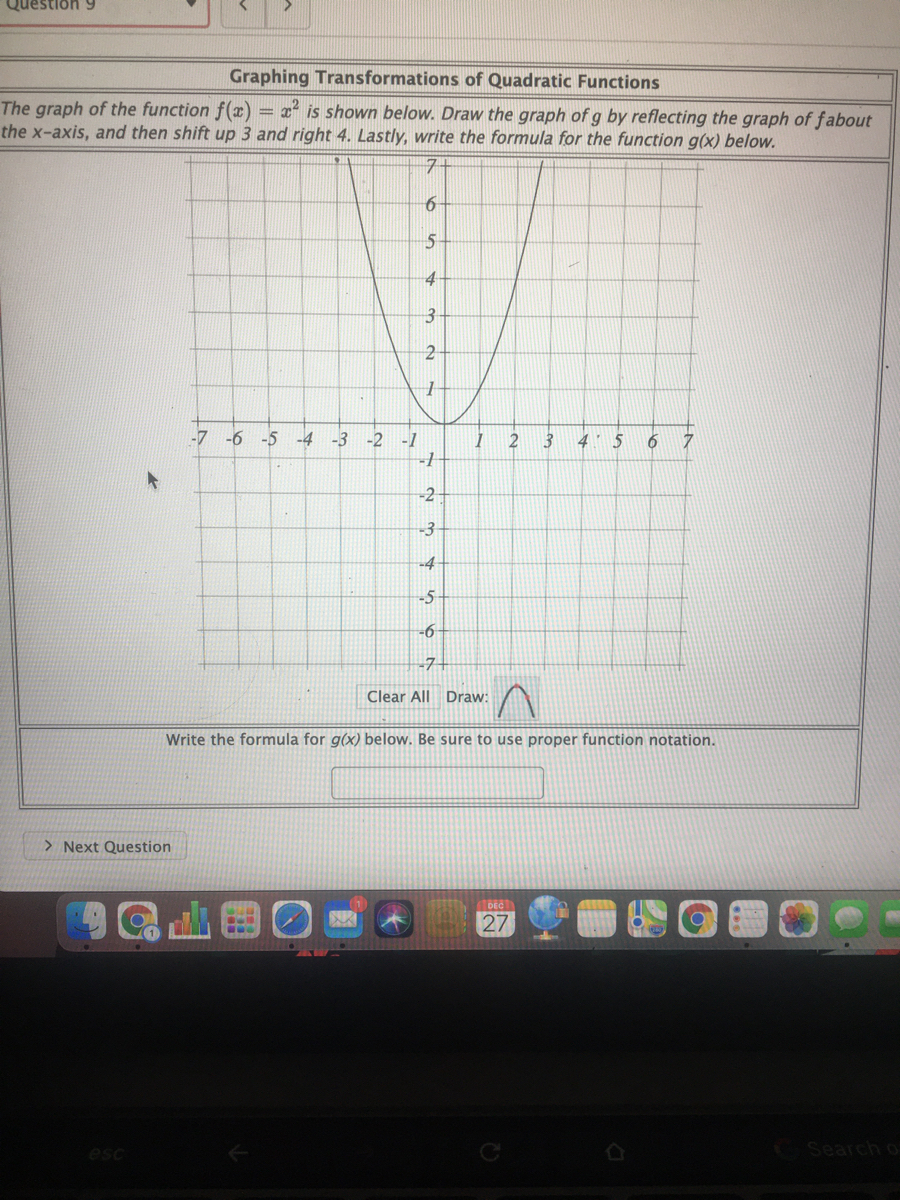



Answered Graphing Transformations Of Quadratic Bartleby
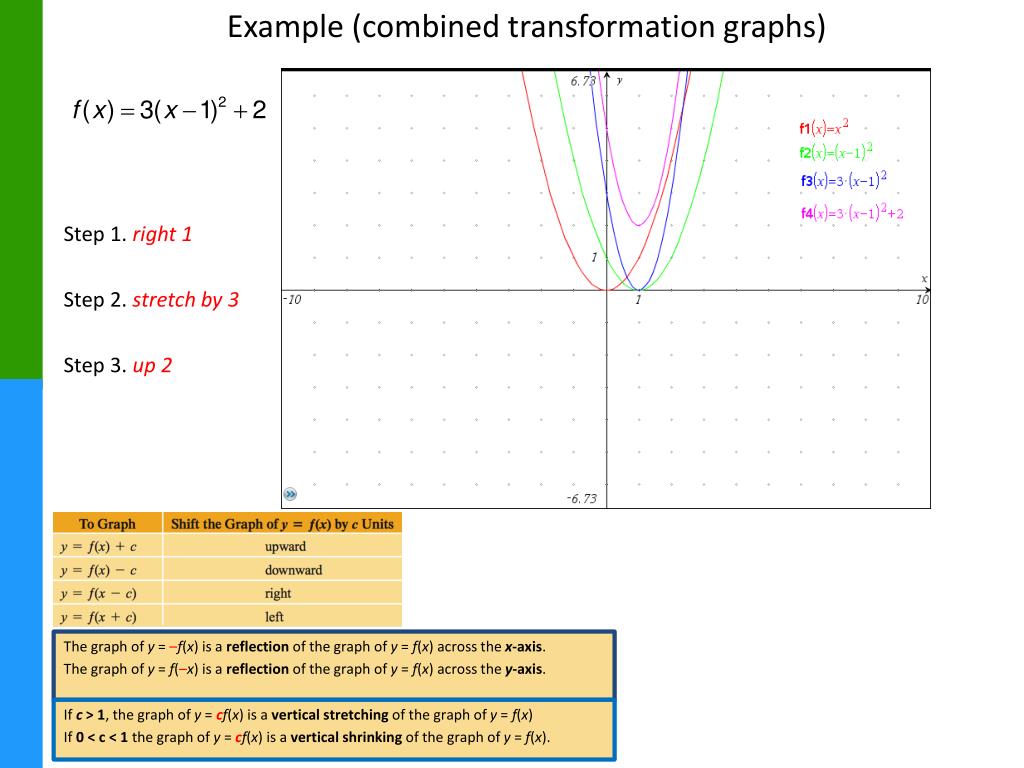



Ppt Transformations Of Graphs Powerpoint Presentation Free Download Id
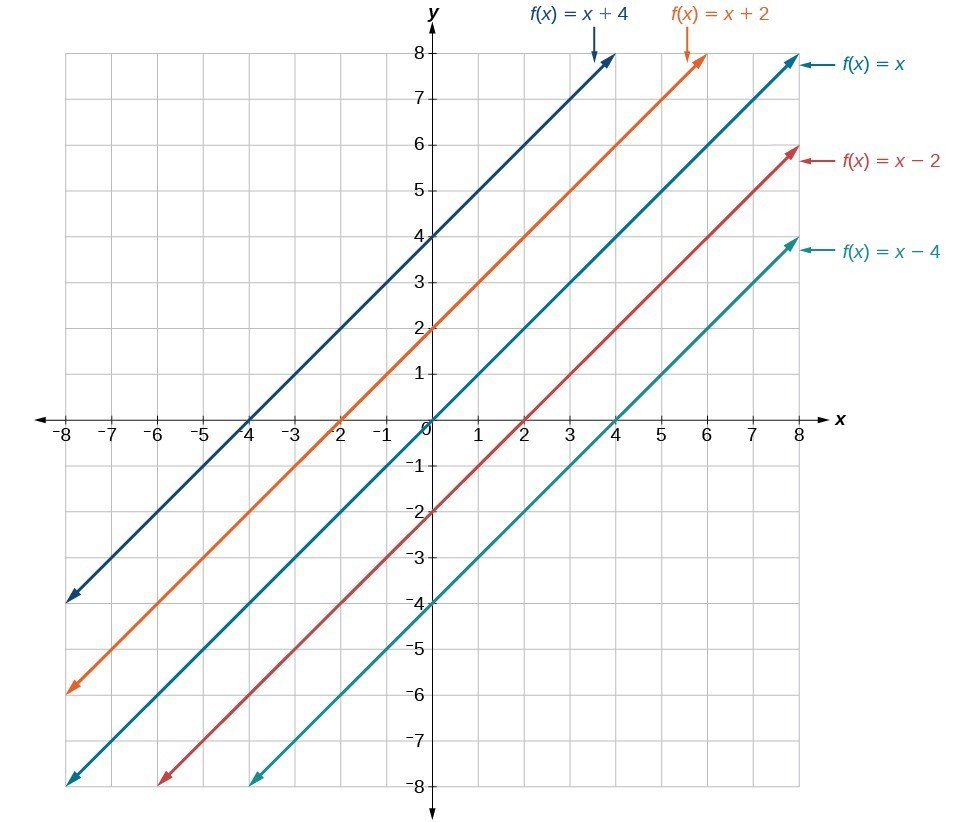



Read Transform Linear Functions Intermediate Algebra
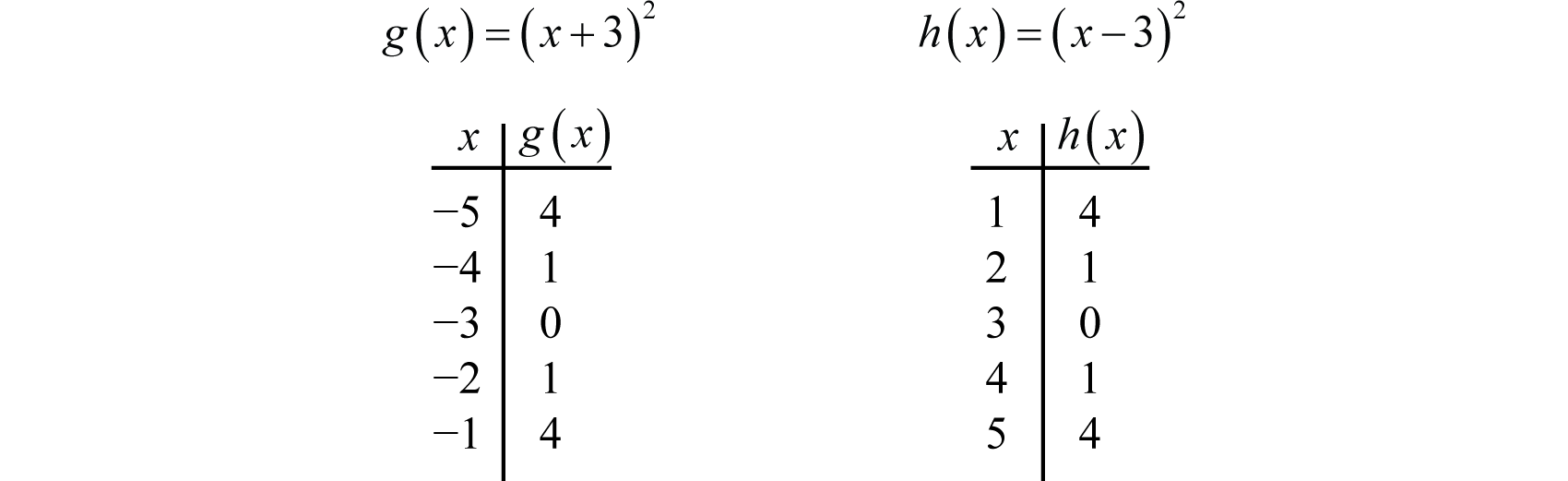



Using Transformations To Graph Functions




Graph A Represents The Function F X Root 3 X Graph B And Graph C Transformations Of Graph A Brainly Com




The Function F X Is Shown On The Provided Graph Graph The Result Of The Following Transformation On Brainly Com




Solved A Graphs Of Logarithmic Functions 1 Let G X L Chegg Com




Reflecting Compressing Functions Video Khan Academy




Begin By Graphing The Absolute Value Function F X Chegg Com




Answered Graph The Function F X 4x 8x 3 By Bartleby



Geogebra Tutorial Functions



Transforming Graphs F G X Geogebra



0 件のコメント:
コメントを投稿